
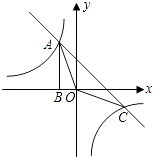
【题目】如图,Rt△ABO的顶点A是双曲线y= ![]() 与直线y=﹣x﹣(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=
与直线y=﹣x﹣(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO= ![]() .
.
(1)求这两个函数的解析式;
(2)求直线与双曲线的两个交点A、C的坐标和△AOC的面积.
【答案】
(1)解:设A点坐标为(x,y),且x<0,y>0, 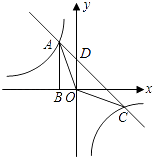
则S△ABO= ![]() |BO||BA|=
|BO||BA|= ![]() (﹣x)y=
(﹣x)y= ![]() ,
,
∴xy=﹣3,
又∵y= ![]() ,
,
即xy=k,
∴k=﹣3.
∴所求的两个函数的解析式分别为y=﹣ ![]() ,y=﹣x+2;
,y=﹣x+2;
(2)解:由y=﹣x+2,
令x=0,得y=2.
∴直线y=﹣x+2与y轴的交点D的坐标为(0,2),
A、C两点坐标满足 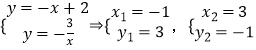
∴交点A为(﹣1,3),C为(3,﹣1),
∴S△AOC=S△ODA+S△ODC= ![]() OD(|x1|+|x2|)=
OD(|x1|+|x2|)= ![]() ×2×(3+1)=4.
×2×(3+1)=4.
【解析】两解析式的k一样,根据面积计算双曲线中的k较易,由公式![]() =2S△ABO,可求出k;(2)求交点就求两解析式联立的方程组的解,可分割△AOC为S△ODA+S△ODC,即可求出.
=2S△ABO,可求出k;(2)求交点就求两解析式联立的方程组的解,可分割△AOC为S△ODA+S△ODC,即可求出.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,已知∠1+∠2=180°,∠3=∠B 求证:∠AED=∠ACB
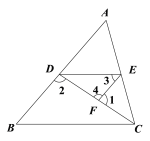
证明:∵∠1+∠4=180°(平角定义)
∠1+∠2=180°(已知)
∴_____________( )
∴ ∥ ( )
∴∠3+∠ =180°( )
又∵∠3=∠B(已知)
∴∠ +∠ =180°(等量代换)
∴ ∥ ( )
∴∠AED=∠ACB( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点A在射线CE上,∠C=∠D.
(1)如图1,若AC∥BD,求证:AD∥BC;
(2)如图2,若∠BAC=∠BAD,BD⊥BC,请探究∠DAE与∠C的数量关系,写出你的探究结论,并加以证明;
(3)如图3,在(2)的条件下,过点D作DF∥BC交射线于点F,当∠DFE=8∠DAE时,求∠BAD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Rt△ABC中,∠C=90°,点D、E分别是△ABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.

(1)若点P在线段AB上,如图(1)所示,且∠α=50°,则∠1+∠2= °;
(2)若点P在边AB上运动,如图(2)所示,则∠α、∠1、∠2之间有何关系?说明理由.
(3)若点P在Rt△ABC斜边BA的延长线上运动(CE<CD),则∠α、∠1、∠2之间有何关系?猜想并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步加强和改进学校体育工作,切实提高学生体质健康水平,决定推进“一校一球队、一级一专项、一人一技能”活动计划,某校决定对学生感兴趣的球类项目(A:足球,B:篮球,C:排球,D:羽毛球,E:乒乓球)进行问卷调查,学生可根据自己的喜好选修一门,李老师对某班全班同学的选课情况进行统计后,制成了两幅不完整的统计图(如图)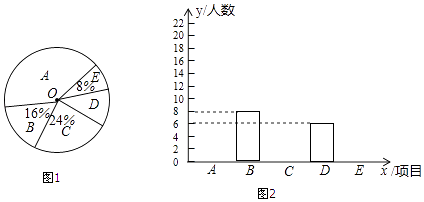
(1)将统计图补充完整
(2)求出该班学生人数
(3)若该校共用学生3500名,请估计有多少人选修足球?
(4)该班班委5人中,1人选修篮球,3人选修足球,1人选修排球,李老师要从这5人中任选2人了解他们对体育选修课的看法,请你用列表或画树状图的方法,求选出的2人恰好1人选修篮球,1人选修足球的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行了“文明在我身边”摄影比赛.已知每幅参赛作品成绩记为x分(60≤x<100).校方从600幅参赛作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制了如下不完整的统计图表.
分数段 | 频数 | 频率 |
60≤x<70 | 18 | 0.36 |
70≤x<80 | 17 | c |
80≤x<90 | a | 0.24 |
90≤x<100 | b | 0.06 |
合计 | 1 |

根据以上信息解答下列问题:
(1)统计表中c的值为________;样本成绩的中位数落在分数段________中;
(2)补全频数直方图;
(3)若80分以上(含80分)的作品将被组织展评,试估计全校被展评的作品数量是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一袋中装有形状大小都相同的四个小球,每个小球上各标有一个数字,分别是1,4,7,8.现规定从袋中任取一个小球,对应的数字作为一个两位数的个位数;然后将小球放回袋中并搅拌均匀,再任取一个小球,对应的数字作为这个两位数的十位数.
(1)写出按上述规定得到所有可能的两位数;
(2)从这些两位数中任取一个,求其算术平方根大于4且小于7的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列叙述中,正确的有( )
①如果![]() ,那么
,那么![]() ;②满足条件
;②满足条件![]() 的n不存在;
的n不存在;
③任意一个三角形的三条高所在的直线相交于一点,且这点一定在三角形的内部;
④ΔABC中,若∠A+∠B=2∠C, ∠A-∠C=40°,则这个△ABC为钝角三角形.
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
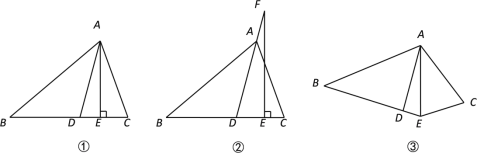
【题目】如图①,![]() 平分
平分![]() ,
,![]() ⊥
⊥![]() ,∠B=450,∠C=730.
,∠B=450,∠C=730.
(1) 求![]() 的度数;
的度数;
(2) 如图②,若把“![]() ⊥
⊥![]() ”变成“点F在DA的延长线上,
”变成“点F在DA的延长线上,![]() ”,其它条件不变,求
”,其它条件不变,求![]() 的度数;
的度数;
(3) 如图③,若把“![]() ⊥
⊥![]() ”变成“
”变成“![]() 平分
平分![]() ”,其它条件不变,
”,其它条件不变,![]() 的大小是否变化,并请说明理由.
的大小是否变化,并请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com