
【题目】已知:如图,已知∠1+∠2=180°,∠3=∠B 求证:∠AED=∠ACB
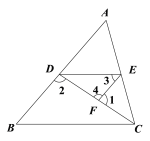
证明:∵∠1+∠4=180°(平角定义)
∠1+∠2=180°(已知)
∴_____________( )
∴ ∥ ( )
∴∠3+∠ =180°( )
又∵∠3=∠B(已知)
∴∠ +∠ =180°(等量代换)
∴ ∥ ( )
∴∠AED=∠ACB( ).
【答案】∠4=∠2,同角的补角相等;BD∥EF,内错角相等,两直线平行;∠BDE ,两直线平行,同旁内角互补;∠B+∠BDE=180°;DE∥BC,同旁内角互补,两直线平行;两直线平行,同位角相等.
【解析】
根据平角的定义及已知,利用同角的补角相等得到∠4=∠2,根据内错角相等,两直线平行得到BD∥EF,根据两直线平行,同旁内角互补得到∠3+∠BDE=180°,等量代换得到∠B+∠BDE=180°,根据同旁内角互补,两直线平行得到DE∥BC,最后根据两直线平行,同位角相等得出结论.
∵∠1+∠4=180°(平角定义)
∠1+∠2=180°(已知)
∴ ∠4=∠2 (同角的补角相等)
∴BD∥ EF( 内错角相等,两直线平行 )
∴∠3+∠ BDE =180°( 两直线平行,同旁内角互补 )
又∵∠3=∠B(已知)
∴∠ B +∠ BDE =180°(等量代换)
∴ DE ∥ BC ( 同旁内角互补,两直线平行 )
∴∠AED=∠ACB( 两直线平行,同位角相等 ).


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
【题目】小明和小亮玩一个游戏:取三张大小、质地都相同的卡片,上面分别标有数字2,3,4(背面完全相同),现将标有数字的一面朝下.小明从中任意抽取一张,记下数字后放回洗匀,然后小亮从中任意抽取一张,计算小明和小亮抽得的两个数字之和.
(1)请你用画树状图或列表的方法,求出这两数和为6的概率.
(2)如果和为奇数,则小明胜;若和为偶数,则小亮胜.你认为这个游戏规则对双方公平吗?做出判断,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知a+b=﹣![]() ,求代数式(a﹣1)2+b(2a+b)+2a的值.
,求代数式(a﹣1)2+b(2a+b)+2a的值.
(2)已知a,b,c是三角形的三边,且a2+b2+c2﹣ab﹣bc﹣ac=0.求证:此三角形是等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
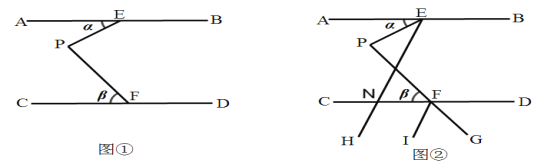
【题目】如图①,已知AB∥CD,点E、F分别是AB、CD上的点,点P是两平行线之间的一点,设∠AEP=α,∠PFC=β,在图①中,过点E作射线EH交CD于点N,作射线FI,延长PF到G,使得PE、FG分别平分∠AEH、∠DFI,得到图②.
(1)在图①中,当α=20°,β=50°时,求∠EPF的度数;
(2)在(1)的条件下,求图②中∠END与∠CFI的度数;
(3)在图②中,当FI∥EH时,请求出α与β的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)实施新课程改革后,学生的自主学习、合作交流能力有很大提高,张老师为了了解所教班级学生自主学习、合作交流的具体情况,对本班部分学生进行了为期三个月的跟踪调查,并将调查结果分成四类,A:特别好;B:好;C:一般;D:较差;并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:

(1)本次调查中,张老师一共调查了 名同学,其中C类女生有 名,D类男生有 名;
(2)将上面的条形统计图补充完整;
(3)为了共同进步,张老师想从被调查的A类和D类学生中分别选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索研究:已知:△ABC和△CDE都是等边三角形.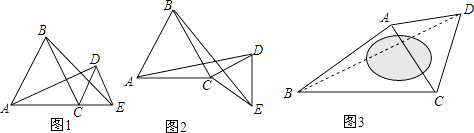
(1)如图1,若点A、C、E在一条直线上时,我们可以得到结论:线段AD与BE的数量关系为: ,
线段AD与BE所成的锐角度数为°;
(2)如图2,当点A、C、E不在一条直线上时,请证明(1)中的结论仍然成立;
灵活运用:
如图3,某广场是一个四边形区域ABCD,现测得:AB=60m,BC=80m,且∠ABC=30°,∠DAC=∠DCA=60°,试求水池两旁B、D两点之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,是一个长为 2m,宽为 2n 的长方形,沿图中虚线用剪刀将其均分成四个完全相同的小长方形,然后按图 2 的形状拼图.
(1)图 2 中的图形阴影部分的边长为 ;(用含 m、n 的代数式表示)
(2)请你用两种不同的方法分别求图 2 中阴影部分的面积; 方法一: ;方法二: .
(3)观察图 2,请写出代数式(m+n)2、(m﹣n)2、4mn 之间的关系式: .

查看答案和解析>>
科目:初中数学 来源: 题型:
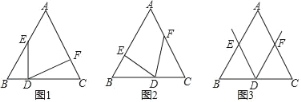
【题目】[感知]
如图①,△ABC是等边三角形,D是边BC上一点(点D不与点B、C重合),作∠EDF=60°,使角的两边分别交边AB、AC于点E、F,且BD=CF.若DE⊥BC,则∠DFC的大小是 度;
[探究]
如图②,△ABC是等边三角形,D是边BC上一点(点D不与点B、C重合),作∠EDF=60°,使角的两边分别交边AB、AC于点E、F,且BD=CF.求证:BE=CD;
[应用]
在图③中,若D是边BC的中点,且AB=2,其它条件不变,如图③所示,则四边形AEDF的周长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABO的顶点A是双曲线y= ![]() 与直线y=﹣x﹣(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=
与直线y=﹣x﹣(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO= ![]() .
.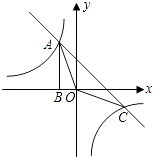
(1)求这两个函数的解析式;
(2)求直线与双曲线的两个交点A、C的坐标和△AOC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com