
【题目】已知:如图1,过等腰直角三角形ABC的直角顶点A作直线AP,点B关于直线AP的对称点为E,连接BE,CE,其中CE交直线AP于点F.
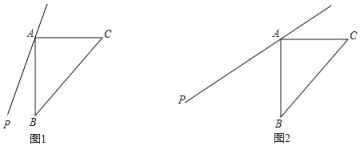
(1)依题意补全图形;
(2)若∠PAB=16°,求∠ACF的度数;
(3)如图2,若45°<∠PAB<90°,用等式表示线段AB,FE,FC之间的数量关系,并证明.
【答案】(1)详见解析;(2)29°;(3)FE2+FC2=2AB2
【解析】
(1)根据题意补全图形;
(2)连接AE,根据轴对称的性质和等腰直角三角形的性质,可得AE=AB,∠EAP=∠BAP=16°,AE=AC=AB,根据三角形的内角和可求∠ACF的度数;
(3)连接AE,BF,设BF交AC于点G,根据轴对称的性质可得AE=AB,FE=FB,可证△AEF≌△ABF,可得∠FEA=∠FBA,根据等腰三角形的性质可得∠ACE=∠ABF,即可求∠CFB=∠BAC=90°,根据勾股定理可得线段AB,FE,FC之间的数量关系.
解:(1)补全图形,如图所示.

(2)如图,连接AE,
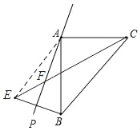
∵点E与点B关于直线AP对称,
∴对称轴AP是EB的垂直平分线.
∴AE=AB,∠EAP=∠BAP=16°,
∵等腰直角三角形ABC,
∴AB=AC,∠BAC=90°,
∴AE=AC,
∴∠AEC=∠ACF
∴2∠ACF+32°+90°=180°,
∴∠ACF=29°,
(3)AB,FE,FC满足的数量关系:FE2+FC2=2AB2,
理由如下:连接AE,BF,设BF交AC于点G,
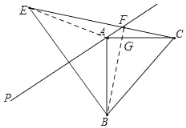
∵点E与点B关于直线AP对称,
∴对称轴AP是EB的垂直平分线,
∴AE=AB,FE=FB,
又∵AF=AF,
∴△AEF≌△ABF(SSS),
∴∠FEA=∠FBA,
∵AB=AC,
∴AE=AC,
∴∠ACE=∠AEC,
∴∠ACE=∠ABF,
又∵∠CGF=∠AGB,
∴∠CFB=∠BAC=90°,
∴FB2+FC2=BC2.
∵BC2=2AB2,
∴FE2+FC2=2AB2


科目:初中数学 来源: 题型:
【题目】已知a,b,c为△ABC的三条边的长,且满足b2+2ab=c2+2ac.
(1)试判断△ABC的形状,并说明理由;
(2)若a=6,b=5,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知AB∥CD,点E、F分别是AB、CD上的点,点P是两平行线之间的一点,设∠AEP=α,∠PFC=β,在图①中,过点E作射线EH交CD于点N,作射线FI,延长PF到G,使得PE、FG分别平分∠AEH、∠DFI,得到图②.
(1)在图①中,当α=20°,β=50°时,求∠EPF的度数;
(2)在(1)的条件下,求图②中∠END与∠CFI的度数;
(3)在图②中,当FI∥EH时,请求出α与β的数量关系.
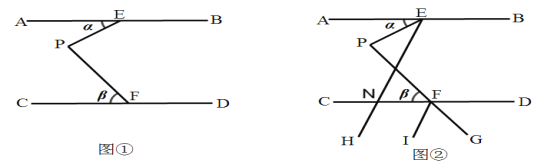
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索研究:已知:△ABC和△CDE都是等边三角形.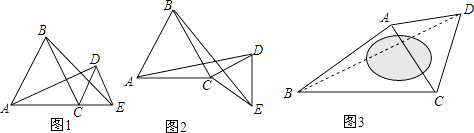
(1)如图1,若点A、C、E在一条直线上时,我们可以得到结论:线段AD与BE的数量关系为: ,
线段AD与BE所成的锐角度数为°;
(2)如图2,当点A、C、E不在一条直线上时,请证明(1)中的结论仍然成立;
灵活运用:
如图3,某广场是一个四边形区域ABCD,现测得:AB=60m,BC=80m,且∠ABC=30°,∠DAC=∠DCA=60°,试求水池两旁B、D两点之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,是一个长为 2m,宽为 2n 的长方形,沿图中虚线用剪刀将其均分成四个完全相同的小长方形,然后按图 2 的形状拼图.
(1)图 2 中的图形阴影部分的边长为 ;(用含 m、n 的代数式表示)
(2)请你用两种不同的方法分别求图 2 中阴影部分的面积; 方法一: ;方法二: .
(3)观察图 2,请写出代数式(m+n)2、(m﹣n)2、4mn 之间的关系式: .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为F,连接DE.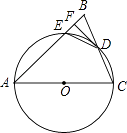
(1)求证:直线DF与⊙O相切;
(2)若AE=7,BC=6,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[感知]
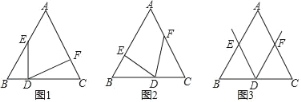
如图①,△ABC是等边三角形,D是边BC上一点(点D不与点B、C重合),作∠EDF=60°,使角的两边分别交边AB、AC于点E、F,且BD=CF.若DE⊥BC,则∠DFC的大小是 度;
[探究]
如图②,△ABC是等边三角形,D是边BC上一点(点D不与点B、C重合),作∠EDF=60°,使角的两边分别交边AB、AC于点E、F,且BD=CF.求证:BE=CD;
[应用]
在图③中,若D是边BC的中点,且AB=2,其它条件不变,如图③所示,则四边形AEDF的周长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图所示,D为BC上一点,且AB=AC=BD,则图中∠1与∠2的关系是( )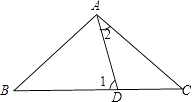
A.∠1=2∠2
B.∠1+∠2=180°
C.∠1+3∠2=180°
D.3∠1﹣∠2=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着出行方式的多样化,某地区打车有三种乘车方式,收费标准如下(假设打车的平均车速为30千米/小时):
网约出租车 | 网约顺风车 | 网约专车 |
3千米以内:12元 | 1.5元/千米 | 2元/千米 |
超过3千米的部分:2.4元/千米 | 0.5元/分钟 | 0.6元/分钟 |
(如:乘坐6千米,耗时12分钟,网约出租车的收费为:12+2.4×(6-3)=19.2(元);网约顺风车的收费为:6×1.5+12×0.5=15(元);网约专车的收费为:6×2+12×0.6=19.2(元))
请据此信息解决如下问题:
(1)王老师乘车从纵棹园去汽车站,全程8千米,如果王老师乘坐网约出租车,需要支付的打车费用为______元;
(2)李校长乘车从纵掉园去生态园,乘坐网约顺风车比乘坐网约出租车节省了2元.求从纵棹园去生态园的路程;
(3)网约专车为了和网约顺风车竞争客户,分别推出了优惠方式:网约顺风车对于乘车路程在5千米以上(含5千米)的客户每次收费立减6元;网约专车打车车费一律七五折优惠.对采用哪一种打车方式更合算提出你的建议.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com