
【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为F,连接DE.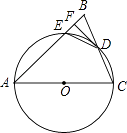
(1)求证:直线DF与⊙O相切;
(2)若AE=7,BC=6,求AC的长.
【答案】
(1)证明:如图,

连接OD.
∵AB=AC,
∴∠B=∠C,
∵OD=OC,
∴∠ODC=∠C,
∴∠ODC=∠B,
∴OD∥AB,
∵DF⊥AB,
∴OD⊥DF,
∵点D在⊙O上,
∴直线DF与⊙O相切;
(2)解:∵四边形ACDE是⊙O的内接四边形,
∴∠AED+∠ACD=180°,
∵∠AED+∠BED=180°,
∴∠BED=∠ACD,
∵∠B=∠B,
∴△BED∽△BCA,
∴ ![]() =
= ![]() ,
,
∵OD∥AB,AO=CO,
∴BD=CD= ![]() BC=3,
BC=3,
又∵AE=7,
∴ ![]() =
= ![]() ,
,
∴BE=2,
∴AC=AB=AE+BE=7+2=9.
【解析】(1)连接OD,利用AB=AC,OD=OC,证得OD∥AD,再证明DF⊥OD,即查得到DF为⊙O的切线;
(2)四边形ACDE是⊙O的内接四边形,∠BED=∠ACD,∠B=∠B,证得△BED∽△BCA,再由相似三角形的性质求得BE的值,最后即可求得AC的长.
【考点精析】本题主要考查了切线的判定定理和相似三角形的判定与性质的相关知识点,需要掌握切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】某校九年级数学兴趣小组为了测得该校地下停车场的限高CD,在课外活动时间测得下列数据:如图,从地面E点测得地下停车场的俯角为30°,斜坡AE的长为16米,地面B点(与E点在同一个水平线)距停车场顶部C点(A、C、B在同一条直线上且与水平线垂直)1.2米.试求该校地下停车场的高度AC及限高CD(结果精确到0.1米).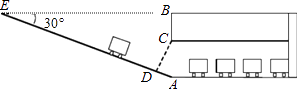
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某营业厅对手机话费业务有如下的优惠:
优惠规则:
①用户手机账户原有话费不能低于240元;
②办理业务时,首先从手机账户中一次性扣除240元,并把这240元抵为300元话费,然后将这300元话费分12次,在每月的15号等额返还到手机账户;
③每月1号从手机账户中扣除话费49元,当月不再扣除其他任何费用;
④每月1号手机账户的话费余额不足以扣除49元时,视为欠费,则当月不再返还等额的话费.
小明的手机账户中原有话费400元,办理了这项优惠业务,设小明的手机账户中每个月末的话费余额是y(元),月数为x(个),则
(1)每个月等额返还的话费是元,第2个月末的话费余额是元;
(2)求y关于x的函数关系式;
(3)若不续费,小明的手机第几个月会欠费?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,过等腰直角三角形ABC的直角顶点A作直线AP,点B关于直线AP的对称点为E,连接BE,CE,其中CE交直线AP于点F.
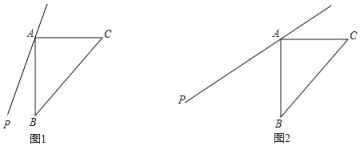
(1)依题意补全图形;
(2)若∠PAB=16°,求∠ACF的度数;
(3)如图2,若45°<∠PAB<90°,用等式表示线段AB,FE,FC之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数。
解:∵EF∥AD,
∴∠2= ( )
又∵∠1=∠2,
∴∠1=∠3,
∴AB∥ ( )
∴∠BAC+ =180°( )
∵∠BAC=70°,∴∠AGD= 。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“世界那么大,我想去看看”一句话红遍网络,骑自行车旅行越来越受人们的喜欢,各种品牌的山地自行车相继投放市场.顺风车行经营的A型车2015年6月份销售总额为3.2万元,2016年经过改造升级后A型车每辆销售价比2015年增加400元,若2016年6月份与2015年6月份卖出的A型车数量相同,则2016年6月份A型车销售总额将比2015年6月份销售总额增加25%.
(1)求2016年6月份A型车每辆销售价为多少元(用列方程的方法解答);
(2)该车行计划2016年7月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,A,B两种型号车的进货和销售价格如下表:
A型车 | B型车 | |
进货价格/(元/辆) | 1100 | 1400 |
销售价格/(元/辆) | 2016年的销售价格 | 2400 |
应如何进货才能使这批车获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ABC的角平分线与∠ACB的外角∠ACD的平分线交于A1.
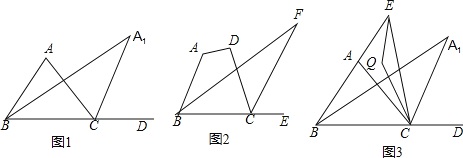
(1)当∠A为70°时,
∵∠ACD -∠ABD=∠____________
∴∠ACD -∠ABD=______________°
∵BA1、CA1是∠ABC的角平分线与∠ACB的外角∠ACD的平分线
∴∠A1CD -∠A1BD=![]() (∠ACD-∠ABD)
(∠ACD-∠ABD)
∴∠A1=___________°;
(2)∠A1BC的角平分线与∠A1CD的角平分线交于A2,∠A2BC与A2CD的平分线交于A3,如此继续下去可得A4、…、An,请写出∠A与∠An 的数量关系____________;
(3)如图2,四边形ABCD中,∠F为∠ABC的角平分线及外角∠DCE的平分线所在的直线构成的角,若∠A+∠D=230度,则∠F= .
(4)如图3,若E为BA延长线上一动点,连EC,∠AEC与∠ACE的角平分线交于Q,当E滑动时有下面两个结论:①∠Q+∠A1的值为定值;②∠Q —∠A1的值为定值.
其中有且只有一个是正确的,请写出正确的结论,并求出其值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com