
【题目】如图,△ABC中,∠ABC的角平分线与∠ACB的外角∠ACD的平分线交于A1.
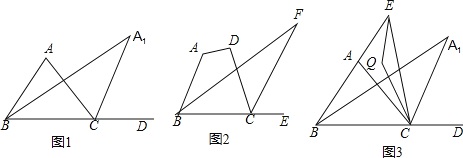
(1)当∠A为70°时,
∵∠ACD -∠ABD=∠____________
∴∠ACD -∠ABD=______________°
∵BA1、CA1是∠ABC的角平分线与∠ACB的外角∠ACD的平分线
∴∠A1CD -∠A1BD=![]() (∠ACD-∠ABD)
(∠ACD-∠ABD)
∴∠A1=___________°;
(2)∠A1BC的角平分线与∠A1CD的角平分线交于A2,∠A2BC与A2CD的平分线交于A3,如此继续下去可得A4、…、An,请写出∠A与∠An 的数量关系____________;
(3)如图2,四边形ABCD中,∠F为∠ABC的角平分线及外角∠DCE的平分线所在的直线构成的角,若∠A+∠D=230度,则∠F= .
(4)如图3,若E为BA延长线上一动点,连EC,∠AEC与∠ACE的角平分线交于Q,当E滑动时有下面两个结论:①∠Q+∠A1的值为定值;②∠Q —∠A1的值为定值.
其中有且只有一个是正确的,请写出正确的结论,并求出其值.
【答案】(1)∠A;70°;35°;
(2)∠A=2n∠An
(3)25°
(4)①∠Q+∠A1的值为定值正确,Q+∠A1=180°.
【解析】试题分析:(1)根据三角形的一个外角等于和它不相邻的两个内角的和的性质填空即可;(2)根据(1)的计算可知∠A=2∠A1由此可知∠A=2n∠An;(3)延长BA、CD交于点M,由∠A+∠D=230°可得∠MAD+∠MDA=130°,根据三角形的内角和定理可得∠M=50°,由(2)的方法可得∠F=25°;(4)根据三角形的一个外角等于和它不相邻的两个内角的和以及角平分线的定义求出表示出∠Q=180°-![]() ∠A与∠A1=
∠A与∠A1=![]() ∠A即可得出结论①是正确的.
∠A即可得出结论①是正确的.
试题解析:
(1)∠A;70°;35°;
(2)∠A=2n∠An
(3)25°
(4)①∠Q+∠A1的值为定值正确.
∵∠ACD﹣∠ABD=∠BAC,BA1、CA1是∠ABC的角平分线与∠ACB的外角∠ACD的平分线
∴∠A1=∠A1CD﹣∠A1BD=![]() ∠BAC,
∠BAC,
∵∠AEC+∠ACE=∠BAC,EQ、CQ是∠AEC、∠ACE的角平分线,
∴∠QEC+∠QCE=![]() (∠AEC+∠ACE)=
(∠AEC+∠ACE)=![]() ∠BAC,
∠BAC,
∴∠Q=180°﹣(∠QEC+∠QCE)=180°﹣![]() ∠BAC,
∠BAC,
∴∠Q+∠A1=180°.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,请探究: 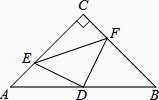
(1)求证:△DFE是等腰直角三角形;
(2)四边形CEDF的面积是否发生变化?若不变化,请求出面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级教师对试卷讲评课中学生参与的深度与广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中学生的参与情况,绘制成如图所示的条形统计图和扇形统计图(均不完整),请根据图中所给信息解答下列问题: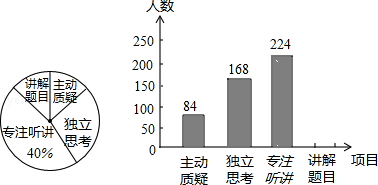
(1)在这次评价中,一共抽查了名学生;
(2)在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为度;
(3)请将条形统计图补充完整;
(4)如果全市有6000名九年级学生,那么在试卷评讲课中,“独立思考”的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列式并计算
(1)求+1.2的相反数与﹣1.3的绝对值的和.
(2)4![]() 与2
与2![]() 的和的相反数.
的和的相反数.
(3)巴黎和北京的时差是﹣7个小时,李伯伯于北京时间9月29号早上8:00搭乘飞往巴黎,飞行时间约11个小时,则李伯伯到达巴黎的时间是 .(填月日时)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是一条直线,OC是∠AOD的平分线,OE在∠BOD内,∠DOE=![]() ∠BOD,∠COE=72°,则∠EOB=( )
∠BOD,∠COE=72°,则∠EOB=( )
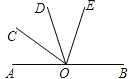
A. 36° B. 72°
C. 108° D. 120°
查看答案和解析>>
科目:初中数学 来源: 题型:
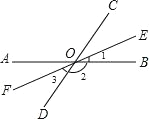
【题目】如图,直线 AB、CD 相交于 O,∠BOC=70°,OE 是∠BOC 的角平分线,OF是OE的反向延长线.
(1)求∠1,∠2,∠3 的度数;
(2)判断 OF 是否平分∠AOD,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
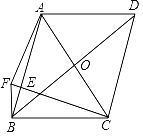
【题目】如图,在ABCD中,对角线AC和BD相交于点O,在AB上有一点E,连接CE,过点B作BC的垂线和CE的延长线交于点F,连接AF,∠ABF=∠FCB,FC=AB,若FB=1,AF=![]() ,则BD=_____.
,则BD=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
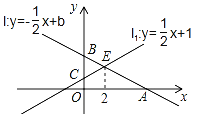
【题目】如图,已知直线l:y=﹣![]() x+b与x轴,y轴的交点分别为A,B,直线l1:y=
x+b与x轴,y轴的交点分别为A,B,直线l1:y=![]() x+1与y轴交于点C,直线l与直线ll的交点为E,且点E的横坐标为2.
x+1与y轴交于点C,直线l与直线ll的交点为E,且点E的横坐标为2.
(1)求实数b的值和点A的坐标;
(2)设点D(a,0)为x轴上的动点,过点D作x轴的垂线,分别交直线l与直线ll于点M、N,若以点B、O、M、N为顶点的四边形是平行四边形,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com