
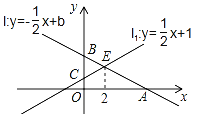
【题目】如图,已知直线l:y=﹣![]() x+b与x轴,y轴的交点分别为A,B,直线l1:y=
x+b与x轴,y轴的交点分别为A,B,直线l1:y=![]() x+1与y轴交于点C,直线l与直线ll的交点为E,且点E的横坐标为2.
x+1与y轴交于点C,直线l与直线ll的交点为E,且点E的横坐标为2.
(1)求实数b的值和点A的坐标;
(2)设点D(a,0)为x轴上的动点,过点D作x轴的垂线,分别交直线l与直线ll于点M、N,若以点B、O、M、N为顶点的四边形是平行四边形,求a的值.
【答案】(1)b=3,A(6,0);(2) a的值为5或﹣1
【解析】
(1)将点E的横坐标为2代入y=![]() x+1求出点E的坐标,再代入y=﹣
x+1求出点E的坐标,再代入y=﹣![]() x+b中可求出b的值,然后令﹣
x+b中可求出b的值,然后令﹣![]() x+b=0解之即可得出A点坐标;
x+b=0解之即可得出A点坐标;
(2)由题可知,MN//OB,只需再求出当MN=OB时的a值,即可得出答案.
(1)∵点E在直线l1上,且点E的横坐标为2,
∴点E的坐标为(2,2),
∵点E在直线l上,
∴![]() ,
,
解得:b=3,
∴直线l的解析式为![]() ,
,
当y=0时,有![]() ,
,
解得:x=6,
∴点A的坐标为(6,0);
(2)如图所示,
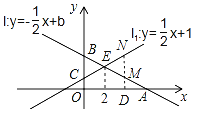
当x=a时,![]() ,
,![]() ,
,
∴![]() ,
,
当x=0时,yB=3,
∴BO=3.
∵BO∥MN,
∴当MN=BO=3时,以点B、O、M、N为顶点的四边形为平行四边形,
此时|2﹣a |=3,
解得:a=5或a=﹣1.
∴当以点B、O、M、N为顶点的四边形为平行四边形,a的值为5或﹣1.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ABC的角平分线与∠ACB的外角∠ACD的平分线交于A1.
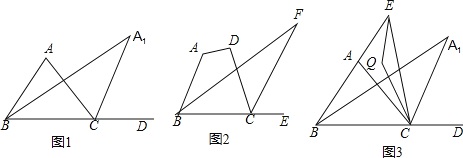
(1)当∠A为70°时,
∵∠ACD -∠ABD=∠____________
∴∠ACD -∠ABD=______________°
∵BA1、CA1是∠ABC的角平分线与∠ACB的外角∠ACD的平分线
∴∠A1CD -∠A1BD=![]() (∠ACD-∠ABD)
(∠ACD-∠ABD)
∴∠A1=___________°;
(2)∠A1BC的角平分线与∠A1CD的角平分线交于A2,∠A2BC与A2CD的平分线交于A3,如此继续下去可得A4、…、An,请写出∠A与∠An 的数量关系____________;
(3)如图2,四边形ABCD中,∠F为∠ABC的角平分线及外角∠DCE的平分线所在的直线构成的角,若∠A+∠D=230度,则∠F= .
(4)如图3,若E为BA延长线上一动点,连EC,∠AEC与∠ACE的角平分线交于Q,当E滑动时有下面两个结论:①∠Q+∠A1的值为定值;②∠Q —∠A1的值为定值.
其中有且只有一个是正确的,请写出正确的结论,并求出其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,点Q为AB边上一点,点F为BC边上一点连接DQ、DF和QF.
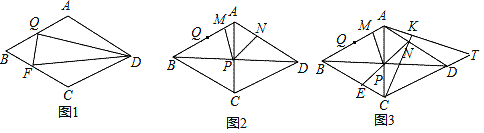
(1)如图1,若∠ADQ=∠FDQ,∠FQD=90°,求证:AQ=BQ;
(2)如图2,在(1)的条件下,∠BAD=120°,对角线AC、BD相交于点P,以点P为顶点作∠MPN=60°,PM与AB交于点M,PN与AD交于点N,求证:DN+QM=AB;
(3)如图3,在(1)(2)的条件下,延长NP交BC于点E,延长CN到点K,使CK=CA,连接AK并延长和CD的延长线交于点T,若AM:DN=1:5,S四边形MBEP=12![]() ,求线段DT的长.
,求线段DT的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家食品公司的市场调查员将本公司生产的一种新点心免费送给50人品尝,以调查这种点心的甜度是否适中.根据调查结果绘制了如下尙不完整的统计图;
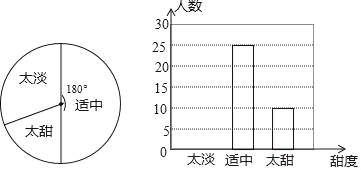
(1)求本次调查中,认为“甜度太甜”的人数占被调查总人数的百分比;
(2)求被调查的50人中,认为“甜度太淡”的人数;
(3)完成条形图;
(4)求扇形图中,“甜度太淡”对应扇形的圆心角度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明、小兵、小颖三人的家和学校在同一条东西走向的路上,星期天,老师到这三家进行家访,从学校出发先向东走 250m 到小明家,后又向东走 350m 到小兵家,再向西行 800m 到小颖家,最后回到学校.
(1)以学校为原点,画出数轴并在数轴上分别表示出小明、小兵、小颖家的位置;
(2)小明家距离小颖家多远?
(3)这次家访,老师共走了多少千米的路程?
查看答案和解析>>
科目:初中数学 来源: 题型:
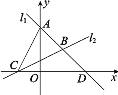
【题目】如图,直线l1过点A(0,4)与点D(4,0),直线l2:y=![]() x+1与x轴交于点C,两直线l1,l2相交于点B.
x+1与x轴交于点C,两直线l1,l2相交于点B.
(1)求直线l1的函数表达式;
(2)求点B的坐标;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们常见的炒菜锅和锅盖都是抛物面,经过锅心和盖心的纵断面是由两段抛物线组合而成的封闭图形,不妨简称为“锅线”.锅口直径为6dm,锅深3dm,锅盖高1dm(锅口直径与锅盖直径视为相同),建立直角坐标系如图1所示,如果把锅纵断面的抛物线记为C1 , 把锅盖纵断面的抛物线记为C2 . 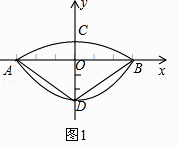
(1)求C1和C2的解析式;
(2)如图2,过点B作直线BE:y= ![]() x﹣1交C1于点E(﹣2,﹣
x﹣1交C1于点E(﹣2,﹣ ![]() ),连接OE、BC,在x轴上求一点P,使以点P、B、C为顶点的△PBC与△BOE相似,求出P点的坐标;
),连接OE、BC,在x轴上求一点P,使以点P、B、C为顶点的△PBC与△BOE相似,求出P点的坐标;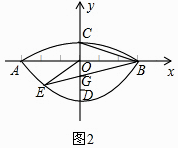
(3)如果(2)中的直线BE保持不变,抛物线C1或C2上是否存在一点Q,使得△EBQ的面积最大?若存在,求出Q的坐标和△EBQ面积的最大值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了对学生进行爱国主义教育,某校组织学生去看演出,有甲乙两种票,已知甲乙两种票的单价比为4:3,单价和为42元.
(1)甲乙两种票的单价分别是多少元?
(2)学校计划拿出不超过750元的资金,让七年级一班的36名学生首先观看,且规定购买甲种票必须多于15张,有哪几种购买方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com