练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，AB是一条直线，OC是∠AOD的平分线，OE在∠BOD内，∠DOE=∠BOD，∠COE=72°，则∠EOB=（ ）

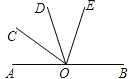
    A. 36° B. 72°

    C. 108° D. 120°

    【答案】B

    【解析】

    设∠DOE=x，根据题意得到∠BOE=2x，∠AOC=∠COD=72°﹣x，再根据平角为180度，得到2×（72°﹣x）+3x=180°，解得x=36°，即可得到∠BOE的度数．

    解：如图，设∠DOE=x，

    ∵∠DOE=∠BOD，

    ∴∠BOE=2x，

    又∵OC是∠AOD的平分线，∠COE=72°，

    ∴∠AOC=∠COD=72°﹣x；

    ∴2×（72°﹣x）+3x=180°，

    解得x=36°，

    ∴∠BOE=2x=2×36°=72°．

    故选B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】下列说法正确的是（　　）

    ①最大的负整数是﹣1；②数轴上表示数2 和﹣2的点到原点的距离相等；③当a≤0时，|a|=﹣a成立；④a的倒数是；⑤（﹣2）2 和﹣22相等．

    A. 2 个 B. 3 个 C. 4 个 D. 5 个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

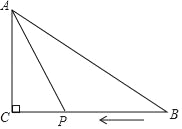
    【题目】如图，在三角形ABC中，∠C＝90°，AC＝6cm，BC＝10cm，点P从B点开始向C点运动速度是每秒1cm，设运动时间是t秒，

    （1）用含t的代数式来表示三角形ACP的面积．

    （2）当三角形ACP的面积是三角形ABC的面积的一半时，求t的值，并指出此时点P在BC上的什么位置？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列说法不正确的有（　　）

    ①一个三角形至少有2个锐角；②在△ABC中，若∠A=2∠B=3∠C，则△ABC为直角三角形；③过n边形的一个顶点可作（n﹣3）条对角线；④n边形每增加一条边，则其内角和增加360°．

    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，∠ABC的角平分线与∠ACB的外角∠ACD的平分线交于A1．

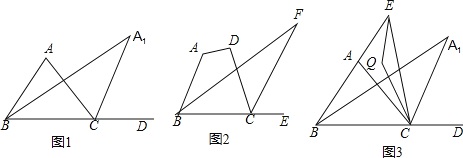
    （1）当∠A为70°时，

    ∵∠ACD －∠ABD=∠____________

    ∴∠ACD －∠ABD=______________°

    ∵BA1、CA1是∠ABC的角平分线与∠ACB的外角∠ACD的平分线

    ∴∠A1CD －∠A1BD=（∠ACD－∠ABD）

    ∴∠A1=___________°；

    （2）∠A1BC的角平分线与∠A1CD的角平分线交于A2，∠A2BC与A2CD的平分线交于A3，如此继续下去可得A4、…、An，请写出∠A与∠An 的数量关系____________；

    （3）如图2，四边形ABCD中，∠F为∠ABC的角平分线及外角∠DCE的平分线所在的直线构成的角，若∠A+∠D=230度，则∠F=　　．

    （4）如图3，若E为BA延长线上一动点，连EC，∠AEC与∠ACE的角平分线交于Q，当E滑动时有下面两个结论：①∠Q+∠A1的值为定值；②∠Q —∠A1的值为定值.

    其中有且只有一个是正确的，请写出正确的结论，并求出其值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，lA，lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系．

    （1）B出发时与A相距______千米．

    （2）B走了一段路后，自行车发生故障，进行修理，所用的时间是______小时．

    （3）B出发后______小时与A相遇．

    （4）若B的自行车不发生故障，保持出发时的速度前进，______小时与A相遇，相遇点离B的出发点______千米．在图中表示出这个相遇点C．

    （5）求出A行走的路程S与时间t的函数关系式。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

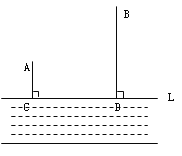
    【题目】如图，A、B两个小集镇在河流CD的同侧，分别到河的距离为AC=10千米，BD=30千米，且CD=30千米，现在要在河边建一自来水厂，向A、B两镇供水，铺设水管的费用为每千米3万，请你在河流CD上选择水厂的位置M，使铺设水管的费用最节省，并求出总费用是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线AB与CD相交于点O，∠AOC=50°，OE平分∠AOD，OF平分∠BOD．

    (1)填空：∠BOD=　 　度；

    (2)试说明OE⊥OF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明、小兵、小颖三人的家和学校在同一条东西走向的路上，星期天，老师到这三家进行家访，从学校出发先向东走 250m 到小明家，后又向东走 350m 到小兵家，再向西行 800m 到小颖家，最后回到学校．

    (1)以学校为原点，画出数轴并在数轴上分别表示出小明、小兵、小颖家的位置；

    (2)小明家距离小颖家多远？

    (3)这次家访，老师共走了多少千米的路程？

    查看答案和解析>>

    同步练习册答案