
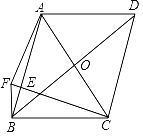
【题目】如图,在ABCD中,对角线AC和BD相交于点O,在AB上有一点E,连接CE,过点B作BC的垂线和CE的延长线交于点F,连接AF,∠ABF=∠FCB,FC=AB,若FB=1,AF=![]() ,则BD=_____.
,则BD=_____.
 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ABC的角平分线与∠ACB的外角∠ACD的平分线交于A1.
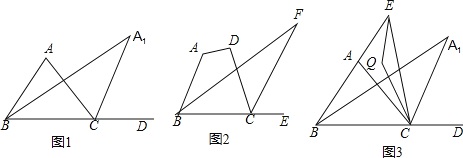
(1)当∠A为70°时,
∵∠ACD -∠ABD=∠____________
∴∠ACD -∠ABD=______________°
∵BA1、CA1是∠ABC的角平分线与∠ACB的外角∠ACD的平分线
∴∠A1CD -∠A1BD=![]() (∠ACD-∠ABD)
(∠ACD-∠ABD)
∴∠A1=___________°;
(2)∠A1BC的角平分线与∠A1CD的角平分线交于A2,∠A2BC与A2CD的平分线交于A3,如此继续下去可得A4、…、An,请写出∠A与∠An 的数量关系____________;
(3)如图2,四边形ABCD中,∠F为∠ABC的角平分线及外角∠DCE的平分线所在的直线构成的角,若∠A+∠D=230度,则∠F= .
(4)如图3,若E为BA延长线上一动点,连EC,∠AEC与∠ACE的角平分线交于Q,当E滑动时有下面两个结论:①∠Q+∠A1的值为定值;②∠Q —∠A1的值为定值.
其中有且只有一个是正确的,请写出正确的结论,并求出其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
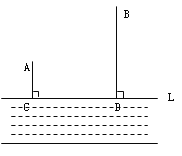
【题目】如图,A、B两个小集镇在河流CD的同侧,分别到河的距离为AC=10千米,BD=30千米,且CD=30千米,现在要在河边建一自来水厂,向A、B两镇供水,铺设水管的费用为每千米3万,请你在河流CD上选择水厂的位置M,使铺设水管的费用最节省,并求出总费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
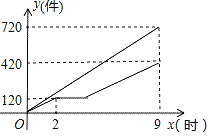
【题目】甲、乙两车间同时开始加工一批零件,从开始加工到加工完这批零件,甲车间工作了9小时,乙车间在中途停工一段时间维修设备,修好后马上按停工前的工作效率继续加工,直到与甲车间同时完成这批零件的加工任务为止,设甲、乙两车间各自加工零件的数量为y(个),甲车间加工的时间为x(时),y与x之间的函数图象如图所示,下列说法其中正确的个数为( )
①这批零件的总个数为1260个;
②甲车间每小时加工零件个数为80个;
③乙车间维修设备后,乙车间加工零件数量y与x之间的函数关系式y=60x﹣120;
④乙车间维修设备用了2个小时
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,点Q为AB边上一点,点F为BC边上一点连接DQ、DF和QF.
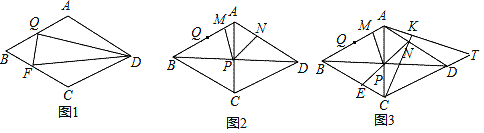
(1)如图1,若∠ADQ=∠FDQ,∠FQD=90°,求证:AQ=BQ;
(2)如图2,在(1)的条件下,∠BAD=120°,对角线AC、BD相交于点P,以点P为顶点作∠MPN=60°,PM与AB交于点M,PN与AD交于点N,求证:DN+QM=AB;
(3)如图3,在(1)(2)的条件下,延长NP交BC于点E,延长CN到点K,使CK=CA,连接AK并延长和CD的延长线交于点T,若AM:DN=1:5,S四边形MBEP=12![]() ,求线段DT的长.
,求线段DT的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家食品公司的市场调查员将本公司生产的一种新点心免费送给50人品尝,以调查这种点心的甜度是否适中.根据调查结果绘制了如下尙不完整的统计图;
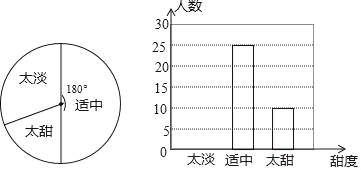
(1)求本次调查中,认为“甜度太甜”的人数占被调查总人数的百分比;
(2)求被调查的50人中,认为“甜度太淡”的人数;
(3)完成条形图;
(4)求扇形图中,“甜度太淡”对应扇形的圆心角度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们常见的炒菜锅和锅盖都是抛物面,经过锅心和盖心的纵断面是由两段抛物线组合而成的封闭图形,不妨简称为“锅线”.锅口直径为6dm,锅深3dm,锅盖高1dm(锅口直径与锅盖直径视为相同),建立直角坐标系如图1所示,如果把锅纵断面的抛物线记为C1 , 把锅盖纵断面的抛物线记为C2 . 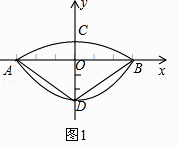
(1)求C1和C2的解析式;
(2)如图2,过点B作直线BE:y= ![]() x﹣1交C1于点E(﹣2,﹣
x﹣1交C1于点E(﹣2,﹣ ![]() ),连接OE、BC,在x轴上求一点P,使以点P、B、C为顶点的△PBC与△BOE相似,求出P点的坐标;
),连接OE、BC,在x轴上求一点P,使以点P、B、C为顶点的△PBC与△BOE相似,求出P点的坐标;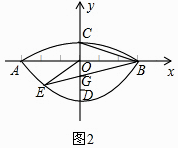
(3)如果(2)中的直线BE保持不变,抛物线C1或C2上是否存在一点Q,使得△EBQ的面积最大?若存在,求出Q的坐标和△EBQ面积的最大值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com