
【题目】甲、乙两车间同时开始加工一批零件,从开始加工到加工完这批零件,甲车间工作了9小时,乙车间在中途停工一段时间维修设备,修好后马上按停工前的工作效率继续加工,直到与甲车间同时完成这批零件的加工任务为止,设甲、乙两车间各自加工零件的数量为y(个),甲车间加工的时间为x(时),y与x之间的函数图象如图所示,下列说法其中正确的个数为( )
①这批零件的总个数为1260个;
②甲车间每小时加工零件个数为80个;
③乙车间维修设备后,乙车间加工零件数量y与x之间的函数关系式y=60x﹣120;
④乙车间维修设备用了2个小时
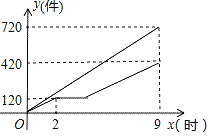
A. 1个 B. 2个 C. 3个 D. 4个
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y= ![]() x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC//x轴,点P是直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC//x轴,点P是直线AC下方抛物线上的动点.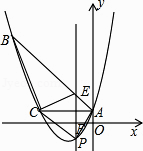
(1)求抛物线的解析式;
(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线 AB、CD 相交于 O,∠BOC=70°,OE 是∠BOC 的角平分线,OF是OE的反向延长线.
(1)求∠1,∠2,∠3 的度数;
(2)判断 OF 是否平分∠AOD,并说明理由.
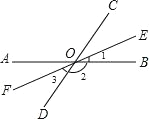
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F. 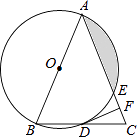
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC和BD相交于点O,在AB上有一点E,连接CE,过点B作BC的垂线和CE的延长线交于点F,连接AF,∠ABF=∠FCB,FC=AB,若FB=1,AF=![]() ,则BD=_____.
,则BD=_____.
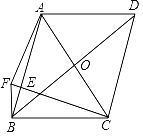
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在四边形ABCD中,∠ABC=∠DCB=90°,点P在BC边上,连接AP和PD,点E在DC边上,连接BE与DP和AP分别交于点F和点G,若AB=PC,BP=DC,∠DFE=45°.
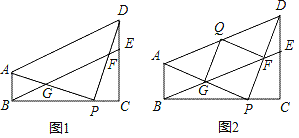
(1)如图1,求证:四边形ABED为平行四边形;
(2)如图2,把△PFG沿FG翻折,得到△QFG(点P与点Q为对应点),点Q在AD上,在不添加任何辅助线的情况下,请直接写出图中所有的平行四边形(不包括平行四边形ABED,但包括特殊的平行四边形).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,新生活超市在端午节前夕购进价格为3元/个的某品牌粽子,根据市场预测,该品牌粽子每个售价4元时,每天能出售500个,并且售价每上涨0.1元,其销售量将减少10个,为了维护消费者利益,物价部门规定,该品牌粽子售价不能超过进价的200%,请你利用所学知识帮助超市给该品牌粽子定价,使超市每天的销售利润为800元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”. 应用:在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点C的极坐标应记为( )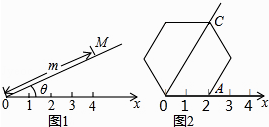
A.(60°,4)
B.(45°,4)
C.(60°,2 ![]() )
)
D.(50°,2 ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com