
【题目】已知:在四边形ABCD中,∠ABC=∠DCB=90°,点P在BC边上,连接AP和PD,点E在DC边上,连接BE与DP和AP分别交于点F和点G,若AB=PC,BP=DC,∠DFE=45°.
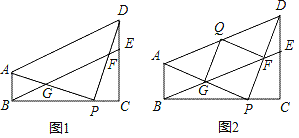
(1)如图1,求证:四边形ABED为平行四边形;
(2)如图2,把△PFG沿FG翻折,得到△QFG(点P与点Q为对应点),点Q在AD上,在不添加任何辅助线的情况下,请直接写出图中所有的平行四边形(不包括平行四边形ABED,但包括特殊的平行四边形).
【答案】(1)证明见解析;(2)四边形AGFQ是平行四边形,四边形QGFD是平行四边形.
【解析】
(1)证明△ABP≌△PCD,可以得出△PAD为等腰直角三角形,得出∠ADP=45°,可得AD∥BE,再证出AB∥DE即可解决问题;
(2)根据平行四边形的判定方法即可判断.
解:(1)∵∠ABC=∠DCB=90°,
∴∠ABC+∠DCB=180°,
∴AB∥CD,
∵AB=PC,BP=DC,
∴△ABP≌△PCD,
∴PA=PD,
∠APD=∠PDC,
∵∠PDC+∠DPC=90°,
∴∠APB+∠DPC=90°,
∴∠APD=90°,
∴△APD是等腰直角三角形,
∴∠ADP=45°,
∵∠DFE=45°,
∴∠ADP=∠DFE,
∴AD∥BE,
∴四边形ABED是平行四边形.
(2)∵∠PGF=∠PAD=45°,∠PFG=∠ADP=45°,
∴△PFG,△FGQ都是等腰直角三角形,
∴四边形PFQG是正方形,
∵∠AGF=135°,∠QFG=∠PFG=45°,
∴∠AGF+∠QFG=180°,
∴AG∥QF,
∵AQ∥FG,
∴四边形AGFQ是平行四边形,
同法可证,四边形QGFD是平行四边形,


科目:初中数学 来源: 题型:
【题目】阅读并理解下面的证明过程,并在每步后的括号内填写该步推理的依据.
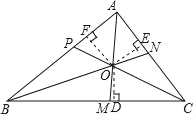
已知:如图,AM,BN,CP是△ABC的三条角平分线.
求证:AM、BN、CP交于一点.
证明:如图,设AM,BN交于点O,过点O分别作OD⊥BC,OF⊥AB,垂足分别为点D,E,F.
∵O是∠BAC角平分线AM上的一点( ),
∴OE=OF( ).
同理,OD=OF.
∴OD=OE( ).
∵CP是∠ACB的平分线( ),
∴O在CP上( ).
因此,AM,BN,CP交于一点.
查看答案和解析>>
科目:初中数学 来源: 题型:
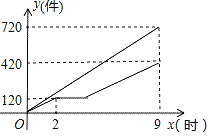
【题目】甲、乙两车间同时开始加工一批零件,从开始加工到加工完这批零件,甲车间工作了9小时,乙车间在中途停工一段时间维修设备,修好后马上按停工前的工作效率继续加工,直到与甲车间同时完成这批零件的加工任务为止,设甲、乙两车间各自加工零件的数量为y(个),甲车间加工的时间为x(时),y与x之间的函数图象如图所示,下列说法其中正确的个数为( )
①这批零件的总个数为1260个;
②甲车间每小时加工零件个数为80个;
③乙车间维修设备后,乙车间加工零件数量y与x之间的函数关系式y=60x﹣120;
④乙车间维修设备用了2个小时
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上点A表示的有理数为﹣6,点B表示的有理数为6,点P从点A出发以每秒4个单位长度的速度在数轴上由A向B运动,当点P到达点B后立即返回,仍然以每秒4个单位长度的速度运动至点A停止运动,设运动时间为t(单位:秒).
(1)求t=1时点P表示的有理数;
(2)求点P与点B重合时的t值;
(3)在点P沿数轴由点A到点B再回到点A的运动过程中,求点P与点A的距离(用含t的代数式表示);
(4)当点P表示的有理数与原点的距离是2个单位长度时,请求出所有满足条件的t值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,点Q为AB边上一点,点F为BC边上一点连接DQ、DF和QF.
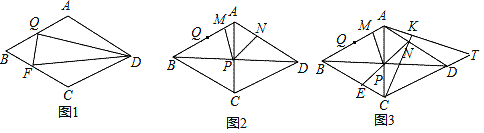
(1)如图1,若∠ADQ=∠FDQ,∠FQD=90°,求证:AQ=BQ;
(2)如图2,在(1)的条件下,∠BAD=120°,对角线AC、BD相交于点P,以点P为顶点作∠MPN=60°,PM与AB交于点M,PN与AD交于点N,求证:DN+QM=AB;
(3)如图3,在(1)(2)的条件下,延长NP交BC于点E,延长CN到点K,使CK=CA,连接AK并延长和CD的延长线交于点T,若AM:DN=1:5,S四边形MBEP=12![]() ,求线段DT的长.
,求线段DT的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,菱形ABCD的顶点A的坐标为(2,0),点B的坐标为(0,1),点C在第一象限,对角线BD与x轴平行.直线y=x+3与x轴、y轴分别交于点E、F.将菱形ABCD沿x轴向左平移m个单位,当点D落在△EOF的内部时(不包括三角形的边),m的取值范围是( )
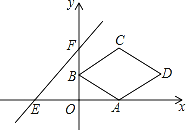
A. 4<m<6 B. 4≤m≤6 C. 4<m<5 D. 4≤m<5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请根据图中提供的信息,回答下列问题

(1)一个暖瓶与一个水杯分别是多少元?
(2)甲、乙两家商场同时出售同样的暖瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定: 这两种商品都打九折;乙商场规定:买一个暖瓶赠送一个水杯。若某单位想要买4个暖瓶和15个水杯,请问选择哪家商场购买更合算,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com