
【题目】如图,在平面直角坐标系xOy中,菱形ABCD的顶点A的坐标为(2,0),点B的坐标为(0,1),点C在第一象限,对角线BD与x轴平行.直线y=x+3与x轴、y轴分别交于点E、F.将菱形ABCD沿x轴向左平移m个单位,当点D落在△EOF的内部时(不包括三角形的边),m的取值范围是( )
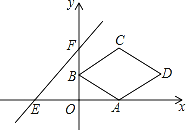
A. 4<m<6 B. 4≤m≤6 C. 4<m<5 D. 4≤m<5
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=![]() AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是( )
AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是( )

A. ①② B. ②③ C. ①③ D. ①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F. 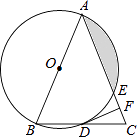
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在四边形ABCD中,∠ABC=∠DCB=90°,点P在BC边上,连接AP和PD,点E在DC边上,连接BE与DP和AP分别交于点F和点G,若AB=PC,BP=DC,∠DFE=45°.
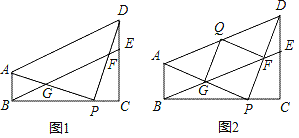
(1)如图1,求证:四边形ABED为平行四边形;
(2)如图2,把△PFG沿FG翻折,得到△QFG(点P与点Q为对应点),点Q在AD上,在不添加任何辅助线的情况下,请直接写出图中所有的平行四边形(不包括平行四边形ABED,但包括特殊的平行四边形).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有三个点A、B、C,完成下列问题:
![]()
(1)将点B向右移动六个单位长度到点D,在数轴上表示出点D.
(2)在数轴上找到点E,使点E为BA的中点(E到A、C两点的距离相等),井在数轴上标出点E表示的数,求出CE的长.
(3)O为原点,取OC的中点M,分OC分为两段,记为第一次操作:取这两段OM、CM的中点分别为了N1、N2,将OC分为4段,记为第二次操作,再取这两段的中点将OC分为8段,记为第三次操作,第六次操作后,OC之间共有多少个点?求出这些点所表示的数的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,新生活超市在端午节前夕购进价格为3元/个的某品牌粽子,根据市场预测,该品牌粽子每个售价4元时,每天能出售500个,并且售价每上涨0.1元,其销售量将减少10个,为了维护消费者利益,物价部门规定,该品牌粽子售价不能超过进价的200%,请你利用所学知识帮助超市给该品牌粽子定价,使超市每天的销售利润为800元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A( ![]() ,1)在反比例函数y=
,1)在反比例函数y= ![]() 的图象上.
的图象上.
(1)求反比例函数y= ![]() 的表达式;
的表达式;
(2)在x轴的负半轴上存在一点P,使得S△AOP= ![]() S△AOB , 求点P的坐标;
S△AOB , 求点P的坐标;
(3)若将△BOA绕点B按逆时针方向旋转60°得到△BDE.直接写出点E的坐标,并判断点E是否在该反比例函数的图象上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇准备完成题目:化简:![]() ,发现系数“
,发现系数“![]() ”印刷不清楚.
”印刷不清楚.
(1)他把“![]() ”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“![]() ”是几?
”是几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是用大小相等的小正方形按一定规律拼成的,则第10个图形是_________个小正方形,第n 个图形是___________个小正方形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com