
【题目】如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=80m,DE=10m,求障碍物B,C两点间的距离(结果精确到0.1m)(参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
【答案】解:如图,过点D作DF⊥AB于点F,过点C作CH⊥DF于点H.
则DE=BF=CH=10m,
在直角△ADF中,∵AF=80m﹣10m=70m,∠ADF=45°,
∴DF=AF=70m.
在直角△CDE中,∵DE=10m,∠DCE=30°,
∴CE= ![]() =
= ![]() =10
=10 ![]() (m),
(m),
∴BC=BE﹣CE=70﹣10 ![]() ≈70﹣17.32≈52.7(m).
≈70﹣17.32≈52.7(m).
答:障碍物B,C两点间的距离约为52.7m.
【解析】通过作垂线把特殊角放在直角三角形中,利用三角函数由边求边,再利用线段之差即可求出BC .
【考点精析】掌握关于仰角俯角问题是解答本题的根本,需要知道仰角:视线在水平线上方的角;俯角:视线在水平线下方的角.


科目:初中数学 来源: 题型:
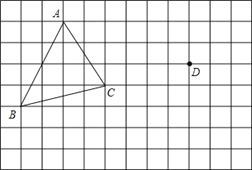
【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC平移,使点A变换为点D,点E、F分别是B、C的对应点.
(1)请画出平移后的△DEF,并求△DEF的面积=
(2)若连接AD、CF,则这两条线段之间的关系是_________________;
(3)请在AB上找一点P,使得线段CP平分△ABC的面积,在图上作出线段CP.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直角坐标系中,A、B、D三点的坐标分别为A(8,0),B(0,4),D(﹣1,0),点C与点B关于x轴对称,连接AB、AC.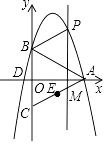
(1)求过A、B、D三点的抛物线的解析式;
(2)有一动点E从原点O出发,以每秒2个单位的速度向右运动,过点E作x轴的垂线,交抛物线于点P,交线段CA于点M,连接PA、PB,设点E运动的时间为t(0<t<4)秒,求四边形PBCA的面积S与t的函数关系式,并求出四边形PBCA的最大面积;
(3)抛物线的对称轴上是否存在一点H,使得△ABH是直角三角形?若存在,请直接写出点H的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:△ABC的周长为30cm,把△ABC的边AC对折,使顶点C和点A重合,折痕交BC边于点D,交AC边与点E,连接AD,若AE=4cm,求△ABD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,B1(0,1),B2(0,3),B3(0,6),B4(0,10),…,以B1B2为对角线作第一个正方形A1B1C1B2,以B2B3为对角线作第二个正方形A2B2C2B3,以B3B4为对角线作第三个正方形A3B3C3B4,…,如果所作正方形的对角线BnBn+1都在y轴上,且BnBn+1的长度依次增加1个单位,顶点An都在第一象限内(n≥1,且n为整数). 那么A1的坐标为____________;An的坐标为_________(用含n的代数式表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好地保护环境,某市污水处理厂决定先购买A,B两型污水处理设备共20台,对周边污水进行处理,每台A型污水处理设备12万元,每台B型污水处理设备10万元.已知2台A型污水处理设备和1台B型污水处理设备每周可以处理污水680吨,4台A型污水处理设备和3台B型污水处理设备每周可以处理污水1560吨.
(1)求A、B两型污水处理设备每周每台分别可以处理污水多少吨?
(2)经预算,市污水处理厂购买设备的资金不超过230万元,每周处理污水的量不低于4500吨,请你列举出所有购买方案.
(3)如果你是厂长,从节约资金的角度来谈谈你会选择哪种方案并说明理由?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC,按如下步骤作图:
步骤1:分别以点A,D为圆心,以大于 ![]() AD的长为半径,在AD两侧作弧,两弧交于点M,N;
AD的长为半径,在AD两侧作弧,两弧交于点M,N;
步骤2:连接MN,分别交AB,AC于点E,F;
步骤3:连接DE,DF.
下列叙述不一定成立的是( )
A.线段DE是△ABC的中位线
B.四边形AFDE是菱形
C.MN垂直平分线段AD
D.![]() =
= ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级数学兴趣小组为了测得该校地下停车场的限高CD,在课外活动时间测得下列数据:如图,从地面E点测得地下停车场的俯角为30°,斜坡AE的长为16米,地面B点(与E点在同一个水平线)距停车场顶部C点(A、C、B在同一条直线上且与水平线垂直)1.2米.试求该校地下停车场的高度AC及限高CD(结果精确到0.1米).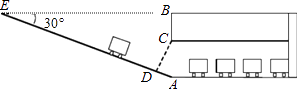
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com