
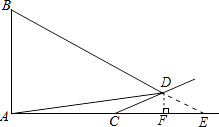
【题目】如图,旗杆AB的顶端B在夕阳的余辉下落在一个斜坡上的点D处,某校数学课外兴趣小组的同学正在测量旗杆的高度,在旗杆的底部A处测得点D的仰角为15°,AC=10米,又测得∠BDA=45°.已知斜坡CD的坡度为i=1: ![]() ,求旗杆AB的高度(
,求旗杆AB的高度( ![]() ,结果精确到个位).
,结果精确到个位).
【答案】解:延长BD,AC交于点E,过点D作DF⊥AE于点F.
∵i=tan∠DCF= ![]() =
= ![]() ,
,
∴∠DCF=30°.
又∵∠DAC=15°,
∴∠ADC=15°.
∴CD=AC=10.
在Rt△DCF中,DF=CDsin30°=10× ![]() =5(米),
=5(米),
CF=CDcos30°=10× ![]() =5
=5 ![]() ,∠CDF=60°.
,∠CDF=60°.
∴∠BDF=45°+15°+60°=120°,
∴∠E=120°﹣90°=30°,
在Rt△DFE中,EF= ![]() =
= ![]() =5
=5 ![]()
∴AE=10+5 ![]() +5
+5 ![]() =10
=10 ![]() +10.
+10.
在Rt△BAE中,BA=AEtanE=(10 ![]() +10)×
+10)× ![]() =10+
=10+ ![]() ≈16(米).
≈16(米).
答:旗杆AB的高度约为16米.
【解析】须把AB、CD放到直角三角形中,须过D点垂线构造直角三角形,利用三角函数由边求边,可求出AB.


科目:初中数学 来源: 题型:
【题目】某生物兴趣小组在四天的实验研究中发现:骆驼的体温会随外部环境温度的变化而变化,而且在这四天中每昼夜的体温变化情况相同,他们将一头骆驼前两昼夜的体温变化情况绘制成右图,请根据图象回答:
(1)在这个问题中,自变量是什么?因变量是什么?
(2)第一天中,在什么时间范围内这头骆驼的体温是上升的?它的体温从最低上升到最高需要多少时间?
(3)第三天12时这头骆驼的体温是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】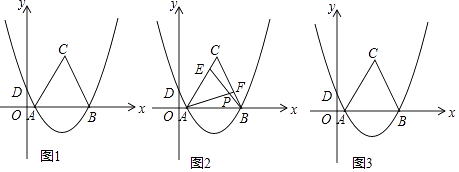
如图1,抛物线y=ax2+bx+ ![]() ,经过A(1,0)、B(7,0)两点,交y轴于D点,以AB为边在x轴上方作等边△ABC.
,经过A(1,0)、B(7,0)两点,交y轴于D点,以AB为边在x轴上方作等边△ABC.
(1)求抛物线的解析式;
(2)在x轴上方的抛物线上是否存在点M,是S△ABM= ![]() S△ABC?若存在,请求出点M的坐标;若不存在,请说明理由;
S△ABC?若存在,请求出点M的坐标;若不存在,请说明理由;
(3)如图2,E是线段AC上的动点,F是线段BC上的动点,AF与BE相交于点P.
①若CE=BF,试猜想AF与BE的数量关系及∠APB的度数,并说明理由;
②若AF=BE,当点E由A运动到C时,请直接写出点P经过的路径长(不需要写过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小美周末来到公园,发现在公园一角有一种“守株待兔”游戏.游戏设计者提供了一只兔子和一个有A,B,C,D,E五个出入口的兔笼,而且笼内的兔子从每个出入口走出兔笼的机会是均等的.规定:①玩家只能将小兔从A,B两个出入口放入,②如果小兔进入笼子后选择从开始进入的出入口离开,则可获得一只价值5元小兔玩具,否则每玩一次应付费3元.
(1)请用表格或树状图求小美玩一次“守株待兔”游戏能得到小兔玩具的概率;
(2)假设有1000人次玩此游戏,估计游戏设计者可赚多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用5个棱长为1的正方体组成如图所示的几何体.
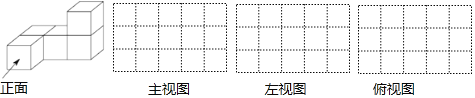
(1)该几何体的体积是多少立方单位,表面积是多少平方单位(包括底面积);
(2)请在方格纸中用实线画出它的三个视图.
查看答案和解析>>
科目:初中数学 来源: 题型:
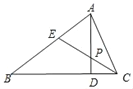
【题目】如图,在△ABC中,AD是△ABC的高线,CE是△ABC的角平分线,它们相交于点P.
(1)若∠B=40°,∠AEC=75°,求证:AB=BC;
(2)若∠BAC=90°,AP为△AEC边EC上中线,求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b的图象经过点A(3,-3),且与直线y=4x-3的交点B在x轴上.
(1)求直线AB对应的函数表达式;
(2)求直线AB与坐标轴所围成的三角形BOC(O为坐标原点,C为直线AB与y轴的交点)的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,在直角坐标系xOy中,A(﹣1,0),B(3,0),将A,B同时分别向上平移2个单位,再向右平移1个单位,得到的对应点分别为D,C,连接AD,BC.

(1)直接写出点C,D的坐标:C ,D ;
(2)四边形ABCD的面积为 ;
(3)点P为线段BC上一动点(不含端点),连接PD,PO.求证:∠CDP+∠BOP=∠OPD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com