
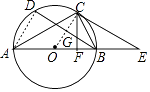
【题目】如图所示,以△ABC的边AB为直径作⊙O,点C在⊙O上,BD是⊙O的弦,∠A=∠CBD,过点C作CF⊥AB于点F,交BD于点G,过C作CE∥BD交AB的延长线于点E.
(1)求证:CE是⊙O的切线;
(2)求证:CG=BG;
(3)若∠DBA=30°,CG=4,求BE的长.
【答案】
(1)证明:连接OC,
∵∠A=∠CBD,
∴ ![]() =
= ![]() ,
,
∴OC⊥BD,
∵CE∥BD,
∴OC⊥CE,
∴CE是⊙O的切线;
(2)证明:∵AB为直径,
∴∠ACB=90°,
∵CF⊥AB,
∴∠ACB=∠CFB=90°,
∵∠ABC=∠CBF,
∴∠A=∠BCF,
∵∠A=∠CBD,
∴∠BCF=∠CBD,
∴CG=BG;
(3)解:连接AD,
∵AB为直径,
∴∠ADB=90°,
∵∠DBA=30°,
∴∠BAD=60°,
∵ ![]() =
= ![]() ,
,
∴∠DAC=∠BAC= ![]() ∠BAD=30°,
∠BAD=30°,
∴ ![]() =tan30°=
=tan30°= ![]() ,
,
∵CE∥BD,
∴∠E=∠DBA=30°,
∴AC=CE,
∴ ![]() =
= ![]() ,
,
∵∠A=∠BCF=∠CBD=30°,
∴∠BCE=30°,
∴BE=BC,
∴△CGB∽△CBE,
∴ ![]() =
= ![]() =
= ![]() ,
,
∵CG=4,
∴BC=4 ![]() ,
,
∴BE=4 ![]() .
.
【解析】(1)连接OC,由两弧再根据垂径定理得到OC⊥BD,根据平行线的性质推出OC⊥CE,CE是⊙O的切线;
(2)先根据圆周角定理得出∠ACB=90°,然后根据同角的余角相等得出∠A=∠BCF,即可证得∠BCF=∠CBD,根据同角对等边即可证得CG=BG;
(3)连接AD,根据圆周角定理得和解直角三角形![]() 的值,再根据三角形相似和等腰三角形的判定即可求得BE的值.
的值,再根据三角形相似和等腰三角形的判定即可求得BE的值.
【考点精析】掌握勾股定理的概念和垂径定理是解答本题的根本,需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.


科目:初中数学 来源: 题型:
【题目】如图,点C是AB的中点,点D是BC的中点,现给出下列等式:①CD=AC-DB,②CD=![]() AB,③CD=AD-BC,④BD=2AD-AB.其中正确的等式编号是( )
AB,③CD=AD-BC,④BD=2AD-AB.其中正确的等式编号是( )
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用5个棱长为1的正方体组成如图所示的几何体.
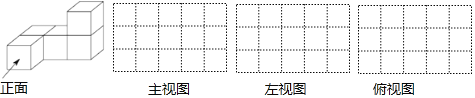
(1)该几何体的体积是多少立方单位,表面积是多少平方单位(包括底面积);
(2)请在方格纸中用实线画出它的三个视图.
查看答案和解析>>
科目:初中数学 来源: 题型:
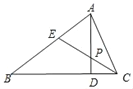
【题目】如图,在△ABC中,AD是△ABC的高线,CE是△ABC的角平分线,它们相交于点P.
(1)若∠B=40°,∠AEC=75°,求证:AB=BC;
(2)若∠BAC=90°,AP为△AEC边EC上中线,求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b的图象经过点A(3,-3),且与直线y=4x-3的交点B在x轴上.
(1)求直线AB对应的函数表达式;
(2)求直线AB与坐标轴所围成的三角形BOC(O为坐标原点,C为直线AB与y轴的交点)的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
求1+2+22+33+…+22018的值.
解:设S=1+2+22+33+…+22018①,
①×2得:2S=2+22+23+…+22018+22019②,
②-①得:2S-S=22019-1,
即S=1+2+22+33+…+22018=22019-1
请你仿照此法计算:
(1)1+2+22+33+24+25=______
(2)1+2+22+33+…+2n______(其中n为正整数)
(3)1+3+32+33+34=______
(4)求1+3+32+33+…+3n的值.(其中n为正整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,AB=6,第一次平移长方形ABCD沿AB的方向向右平移5个单位长度,得到长方形A1B1C1D1,第2次平移长方形A1B1C1D1沿A1B1的方向向右平移5个单位长度,得到长方形A2B2C2D2,…,第n次平移长方形An-1Bn-1Cn-1Dn-1沿An-1Bn-1的方向向右平移5个单位长度,得到长方形AnBnCnDn(n>2),若ABn的长度为2 026,则n的值为( ).
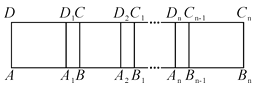
A. 407B. 406C. 405D. 404
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com