
【题目】如图,点O是等边△ABC内一点,D是△ABC外的一点,∠AOB=110°,∠BOC=α,△BOC≌△ADC,∠OCD=60°,连接OD.
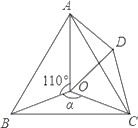
(1)求证:△OCD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当α为多少度时,△AOD是等腰三角形.
【答案】(1)详见解析;(2)△AOD是直角三角形,理由详见解析;(3)当α=110°或125°或140°时,△AOD是等腰三角形.
【解析】
(1)根据全等三角形的性质得到OC=DC,根据等边三角形的判定定理证明即可;
(2)根据全等三角形的性质得到∠ADC=∠BOC=∠α=150°,结合图形计算即可;
(3)分∠AOD=∠ADO、∠AOD=∠OAD、∠ADO=∠OAD三种情况,根据等腰三角形的判定定理计算即可.
解:(1)∵△BOC≌△ADC,
∴OC=DC.
∵∠OCD=60°,
∴△OCD是等边三角形.
(2)△AOD是直角三角形.
理由如下:
∵△OCD是等边三角形,
∴∠ODC=60°,
∵△BOC≌△ADC,∠α=150°,
∴∠ADC=∠BOC=∠α=150°,
∴∠ADO=∠ADC﹣∠ODC=150°﹣60°=90°,
∴△AOD是直角三角形.
(3)∵△OCD是等边三角形,
∴∠COD=∠ODC=60°.
∵∠AOB=110°,∠ADC=∠BOC=α,
∴∠AOD=360°﹣∠AOB﹣∠BOC﹣∠COD=360°﹣110°﹣α﹣60°=190°﹣α,
∠ADO=∠ADC﹣∠ODC=α﹣60°,
∴∠OAD=180°﹣∠AOD﹣∠ADO=180°﹣(190°﹣α)﹣(α﹣60°)=50°.
①当∠AOD=∠ADO时,190°﹣α=α﹣60°,
∴α=125°.
②当∠AOD=∠OAD时,190°﹣α=50°,
∴α=140°.
③当∠ADO=∠OAD时,
α﹣60°=50°,
∴α=110°.
综上所述:当α=110°或125°或140°时,△AOD是等腰三角形.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,点P是等边△ABC的边上的一个做匀速运动的动点,其由点A开始沿AB边运动到B再沿BC边运动到C为止,设运动时间为t,△ACP的面积为S,则S与t的大致图象是( )
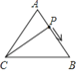
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=4,∠BAC=90°,点D在边AB上,BE∥CD,AE⊥CD,垂足为F,且EF=2,点G在线段CF上,若∠GAF=45°,则△ACG的面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新型冠状病毒爆发,教育部部署了“停课不停学”的有关工作,各地都在进行在线教育.小依同学为了了解网课学习情况,对本班部分同学最喜爱的课程进行了调查,调查课程分别是网上授课、体育锻炼、名著阅读、艺术欣赏和其他课程并制成以下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
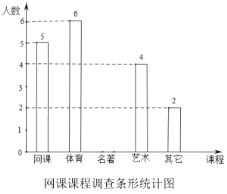
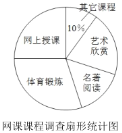
(1)本次调查中一共调查了__________名学生,其中“名著阅读”所占的圆心角度数为__________.
(2)请把条形统计图补全.
(3)在调查的同学中随机选取一名学生,求他恰好最喜爱的课程是“艺术欣赏”的概率.
(4)若该校一共有3000名学生,请估算出全校最喜爱的课程是“体育锻炼”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】锐锐参加我市电视台组织的“牡丹杯”智力竞答节目,答对最后两道单选题就顺利通关,第一道单选题有3个选项,第二道单选题有4个选项,这两道题锐锐都不会,不过锐锐还有两个“求助”可以用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项).
(1)如果锐锐两次“求助”都在第一道题中使用,那么锐锐通关的概率是________;
(2)如果锐锐两次“求助”都在第二道题中使用,那么锐锐通关的概率是________;
(3)如果锐锐每道题各用一次“求助”,请用树状图或者列表来分析他顺利通关的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中,![]() 的顶点都在网格点上,其中,C点坐标为
的顶点都在网格点上,其中,C点坐标为![]() .
.
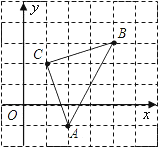
(1)写出点A、B的坐标:
![]() ______ ,______
______ ,______ ![]() 、
、![]() ______ ,______
______ ,______ ![]()
(2)将![]() 先向左平移2个单位长度,再向上平移1个单位长度,得到
先向左平移2个单位长度,再向上平移1个单位长度,得到![]() ,则
,则![]() 的三个顶点坐标分别是
的三个顶点坐标分别是![]() ______ ,______
______ ,______ ![]() 、
、![]() ______ ,______
______ ,______ ![]() 、
、![]() ______ ,______
______ ,______ ![]()
(3)求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为更好地开展“传统文化进校园”活动,随机抽查了部分学生,了解他们最喜爱的传统文化项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布直方图.
最喜爱的传统文化项目类型频数分布表


根据以上信息完成下列问题:
(1)直接写出频数分布表中a的值;
(2)补全频数分布直方图;
(3)若全校共有学生1500名,估计该校最喜爱围棋的学生大约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com