
【题目】新型冠状病毒爆发,教育部部署了“停课不停学”的有关工作,各地都在进行在线教育.小依同学为了了解网课学习情况,对本班部分同学最喜爱的课程进行了调查,调查课程分别是网上授课、体育锻炼、名著阅读、艺术欣赏和其他课程并制成以下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
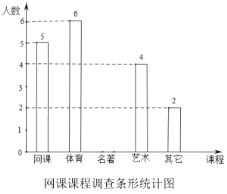
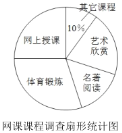
(1)本次调查中一共调查了__________名学生,其中“名著阅读”所占的圆心角度数为__________.
(2)请把条形统计图补全.
(3)在调查的同学中随机选取一名学生,求他恰好最喜爱的课程是“艺术欣赏”的概率.
(4)若该校一共有3000名学生,请估算出全校最喜爱的课程是“体育锻炼”的人数.
【答案】(1)20,![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() ;(4)900人
;(4)900人
【解析】
(1)根据其他课程总人数与所占的百分比即可得出总人数,用总人数减去最喜爱网上授课、体育锻炼、艺术欣赏、其他课程的人数,求出最喜爱名著阅读的人数,从而求出最喜爱名著阅读所占的圆心角度数;
(2)根据(1)求出的最喜爱名著阅读人数,从而补全统计图;;
(3)利用最喜爱艺术欣赏的人数除以总人数即可
(4)用该校的总人数乘以最喜爱的课程是“体育锻炼”的百分比即可.
解:(1)2÷10%=20(名),
即在这次调查中,一共抽取了20名学生;最喜爱名著阅读的人数在:20-5-6-4-2=3(名),
∴最喜爱名著阅读所占的圆心角度数=![]()
(2)补全的条形统计图如图所示;
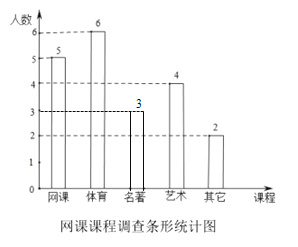
(3)最喜爱艺术欣赏的人数4人,
∴最喜爱的课程是“艺术欣赏”的概率=![]()
(4)![]() (人)
(人)
∴估算出全校最喜爱的课程是“体育锻炼”的人数为900人


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
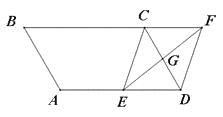
【题目】(7分)如图,平行四边形ABCD中,AB=3cm,BC=5cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.
(1)求证:四边形CEDF是平行四边形;
(2)①当AE= cm时,四边形CEDF是矩形;
②当AE= cm时,四边形CEDF是菱形;(直接写出答案,不需要说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
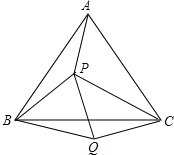
【题目】如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.
(1) 观察并猜想AP与CQ之间的大小关系,并证明你的结论;
(2) 若PA:PB:PC=3:4:5,连接PQ,试判断△PQC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一定能确定△ABC≌△DEF的条件是( )
A.AB=DE,BC=EF,∠A=∠DB.∠A=∠E,AB=EF,∠B=∠D
C.∠A=∠D,AB=DE,∠B=∠ED.∠A=∠D,∠B=∠E,∠C=∠F
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是等边△ABC内一点,D是△ABC外的一点,∠AOB=110°,∠BOC=α,△BOC≌△ADC,∠OCD=60°,连接OD.
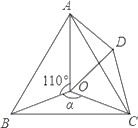
(1)求证:△OCD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当α为多少度时,△AOD是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
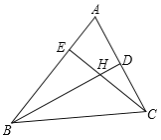
【题目】如图,在△ABC 中,记∠A=x 度,回答下列问题:
(1)图中共有三角形 个.
(2)若 BD,CE 为△ABC 的角平分线,则∠BHC= 度(结果用含 x 的代数式
表示),并证明你的结论.
(3)若 BD,CE 为△ABC 的高线,则∠BHC= 度(结果用含 x 的代数式表示),并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中,抛物线y=mx2﹣2m2x+2交y轴于A点,交直线x=4于B点.
(1)抛物线的对称轴为x=_____(用含m的代数式表示);
(2)若AB∥x轴,求抛物线的表达式;
(3)记抛物线在A,B之间的部分为图象G(包含A,B两点),若对于图象G上任意一点P(xp,yp),yp≤2,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,地面上两个村庄C、D处于同一水平线上,一飞行器在空中以6千米/小时的速度沿MN方向水平飞行,航线MN与C、D在同一铅直平面内.当该飞行器飞行至村庄C的正上方A处时,测得∠NAD=60°;该飞行器从A处飞行40分钟至B处时,测得∠ABD=75°.求村庄C、D间的距离(![]() 取1.73,结果精确到0.1千米)
取1.73,结果精确到0.1千米)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com