
【题目】如图,在△ABC 中,记∠A=x 度,回答下列问题:
(1)图中共有三角形 个.
(2)若 BD,CE 为△ABC 的角平分线,则∠BHC= 度(结果用含 x 的代数式
表示),并证明你的结论.
(3)若 BD,CE 为△ABC 的高线,则∠BHC= 度(结果用含 x 的代数式表示),并证明你的结论.
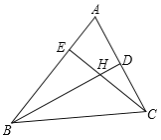
【答案】(1)图中共有三角形 8 个;(2)(90+ ![]() x ) ;(3)(180-x).
x ) ;(3)(180-x).
【解析】
本题考查的是三角形内角和定理,分析题意观察图形,根据三角形内角和为180°可知∠ABC=![]() ,根据角平分线的性质可以求出∠BHC,根据高线的性质可知∠CDB=∠BEC=90,再次利用三角形内角和定理可以求答案
,根据角平分线的性质可以求出∠BHC,根据高线的性质可知∠CDB=∠BEC=90,再次利用三角形内角和定理可以求答案
解:(1)图中共有三角形 8 个;
(2)∠BHC=(90+ ![]() )度.
)度.
∵BD,CE 分别是∠ABC,∠ACB 的平分线,
∴∠BHC=180-∠HBC-∠HCB=180-![]() (∠ABC+∠ACB)= (90+
(∠ABC+∠ACB)= (90+ ![]() )度.
)度.
(3)∠BHC=(180-x)度,
∵BD,CE 为△ABC 的高线,
∴BD⊥AC,CE⊥AB,
∴∠CDB=∠BEC=90,
∵∠BEC+∠ABC+∠BCH=180°
∠CDB+∠ACB+∠CBH=180°
∴∠BEC+∠ABC+∠BCH+∠CDB+∠ACB+∠CBH=360°
∠ABC+∠BCH+∠ACB+∠CBH=180°
∵∠ABC+∠ACB=180°-∠A
∠BCH+∠CBH=180°-∠BHC
∴180°-∠A+180°-∠BHC=180°
∴∠BHC=(180-x)度


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
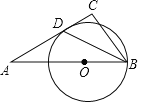
【题目】如图,△ABC中,∠A=30°,点O是边AB上一点,以点O为圆心,以OB为半径作圆,⊙O恰好与AC相切于点D,连接BD.若BD平分∠ABC,AD=2![]() ,则线段CD的长是( )
,则线段CD的长是( )
A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
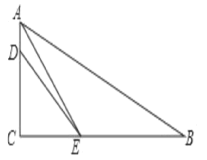
【题目】已知,如图,在Rt△ABC中,∠ACB=90°,AE平分∠BAC交BC于点E,D为AC上的点,BE=DE.
(1)求证:∠B+∠EDA=180°;
(2)求![]() 的值。.
的值。.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.袋中有形状、大小、质地完全一样的5个红球和1个白球,从中随机抽出一个球,一定是红球
B.天气预报“明天降水概率10%”,是指明天有10%的时间会下雨
C.某地发行一种福利彩票,中奖率是千分之一,那么,买这种彩票1000张,一定会中奖
D.连续掷一枚均匀硬币,若5次都是正面朝上,则第六次仍然可能正面朝上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新型冠状病毒爆发,教育部部署了“停课不停学”的有关工作,各地都在进行在线教育.小依同学为了了解网课学习情况,对本班部分同学最喜爱的课程进行了调查,调查课程分别是网上授课、体育锻炼、名著阅读、艺术欣赏和其他课程并制成以下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
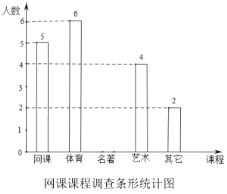
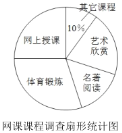
(1)本次调查中一共调查了__________名学生,其中“名著阅读”所占的圆心角度数为__________.
(2)请把条形统计图补全.
(3)在调查的同学中随机选取一名学生,求他恰好最喜爱的课程是“艺术欣赏”的概率.
(4)若该校一共有3000名学生,请估算出全校最喜爱的课程是“体育锻炼”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年暑假,小丽爸爸的同事送给她爸爸一张北京故宫的门票,她和哥哥两人都很想去参观,可门票只有一张.读九年级的哥哥想了一个办法,他拿了八张扑克牌,将数字为1,2,3,5的四张牌给小丽,将数字为4,6,7,8的四张牌留给自己,并按如下游戏规则进行:小利哥哥从各自的四张牌中随机抽出一张,然后将抽出的两张扑克牌上的数字相加,如果和为偶数,和小丽去;如果和为奇数,则哥哥去.
(1)请用画树状图或列表的方法求小丽去北京故宫参观的概率;
(2)哥哥设计的游戏规则公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数y=x2+mx+1,当0<x≤2时的函数值总是非负数,则实数m的取值范围为( )
A. m≥﹣2 B. ﹣4≤m≤﹣2 C. m≥﹣4 D. m≤﹣4或m≥﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一条抛物线的对称轴是直线x=1;它与x轴相交于A,B两点(点A在点B的左边),且线段AB的长是4;它还与过点C(1,﹣2)的直线有一个交点是D(2,﹣3).
(1)求这条直线的函数解析式;
(2)求这条抛物线的函数解析式;
(3)若这条直线上有P点,使S△PAB=12,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.

(1)求证:AB=CF;
(2)连接DE,若AD=2AB,求证:DE⊥AF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com