
【题目】平面直角坐标系xOy中,抛物线y=mx2﹣2m2x+2交y轴于A点,交直线x=4于B点.
(1)抛物线的对称轴为x=_____(用含m的代数式表示);
(2)若AB∥x轴,求抛物线的表达式;
(3)记抛物线在A,B之间的部分为图象G(包含A,B两点),若对于图象G上任意一点P(xp,yp),yp≤2,求m的取值范围.
【答案】(1)m, (2)y=2x2﹣8x+2.(3)m<0或m≥2.
【解析】
(1)根据抛物线的对称轴为直线x=﹣![]() ,代入数据即可得出结论;
,代入数据即可得出结论;
(2)由AB∥x轴,可得出点B的坐标,进而可得出抛物线的对称轴为x=2,结合(1)可得出m=2,将其代入抛物线表达式中即可;
(3)分m>0及m<0两种情况考虑,依照题意画出函数图象,利用数形结合即可得出m的取值范围.
(1)抛物线的对称轴为x=![]() =m.
=m.
故答案为:m.
(2)当x=0时,y=mx2﹣2m2x+2=2,
∴点A(0,2).
∵AB∥x轴,且点B在直线x=4上,
∴点B(4,2),抛物线的对称轴为直线x=2,
∴m=2,
∴抛物线的表达式为y=2x2﹣8x+2.
(3)当m>0时,如图1.
∵A(0,2),
∴要使0≤xp≤4时,始终满足yp≤2,只需使抛物线y=mx2﹣2m2x+2的对称轴与直线x=2重合或在直线x=2的右侧.
∴m≥2;
当m<0时,如图2,
在0≤xp≤4中,yp≤2恒成立.
综上所述,m的取值范围为m<0或m≥2.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中AD是∠A的外角平分线,P是AD上一动点且不与点A、D重合,记PB+PC=a,AB+AC=b,则a、b的大小关系是( )
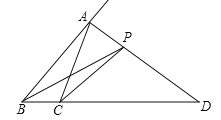
A.a>b B.a=b C.a<b D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新型冠状病毒爆发,教育部部署了“停课不停学”的有关工作,各地都在进行在线教育.小依同学为了了解网课学习情况,对本班部分同学最喜爱的课程进行了调查,调查课程分别是网上授课、体育锻炼、名著阅读、艺术欣赏和其他课程并制成以下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
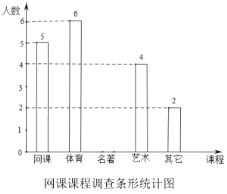
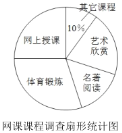
(1)本次调查中一共调查了__________名学生,其中“名著阅读”所占的圆心角度数为__________.
(2)请把条形统计图补全.
(3)在调查的同学中随机选取一名学生,求他恰好最喜爱的课程是“艺术欣赏”的概率.
(4)若该校一共有3000名学生,请估算出全校最喜爱的课程是“体育锻炼”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数y=x2+mx+1,当0<x≤2时的函数值总是非负数,则实数m的取值范围为( )
A. m≥﹣2 B. ﹣4≤m≤﹣2 C. m≥﹣4 D. m≤﹣4或m≥﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中,![]() 的顶点都在网格点上,其中,C点坐标为
的顶点都在网格点上,其中,C点坐标为![]() .
.
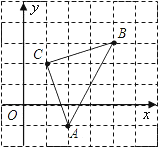
(1)写出点A、B的坐标:
![]() ______ ,______
______ ,______ ![]() 、
、![]() ______ ,______
______ ,______ ![]()
(2)将![]() 先向左平移2个单位长度,再向上平移1个单位长度,得到
先向左平移2个单位长度,再向上平移1个单位长度,得到![]() ,则
,则![]() 的三个顶点坐标分别是
的三个顶点坐标分别是![]() ______ ,______
______ ,______ ![]() 、
、![]() ______ ,______
______ ,______ ![]() 、
、![]() ______ ,______
______ ,______ ![]()
(3)求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一条抛物线的对称轴是直线x=1;它与x轴相交于A,B两点(点A在点B的左边),且线段AB的长是4;它还与过点C(1,﹣2)的直线有一个交点是D(2,﹣3).
(1)求这条直线的函数解析式;
(2)求这条抛物线的函数解析式;
(3)若这条直线上有P点,使S△PAB=12,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
我们可以通过下列步骤估计![]() 的大小.
的大小.
第一步:因为12=1,22=4,1<2<4,所以1<![]() <2.
<2.
第二步:通过取1和2的平均数缩小![]() 所在的范围:取
所在的范围:取![]() ,
,
因为1.52=2.25,2<2.25,所以1<![]() <1.5.
<1.5.
(1)请仿照第一步,通过运算,确定![]() 界于哪两个相邻的整数之间?
界于哪两个相邻的整数之间?
(2)在1<![]() <1.5的基础上,重复应用第二步中取平均数的方法,将
<1.5的基础上,重复应用第二步中取平均数的方法,将![]() 所在的范围缩小至m<
所在的范围缩小至m<![]() <n,使得n-m=
<n,使得n-m=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点.且BE+DF=EF.试求∠EAF度数.
小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得求出∠EAF度数,他求出的∠EAF度数应是 .请你根据他的思路完成论证过程.
(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,试探究当∠EAF与∠BAD满足什么关系时有BE+DF=EF,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10,BC=12,AD=8,AD是BC边上的高.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是( ).
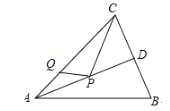
A.6B.8C.9.6D.12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com