
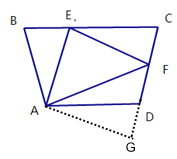
ЁОЬтФПЁП(1)ШчЭМ1,дкЫФБпаЮABCDжаЃЌAB=ADЃЌЁЯBAD=120ЁуЃЌЁЯB=ЁЯADC=90ЁуЃЌEЁЂFЗжБ№ЪЧBCЁЂCDЩЯЕФЕуЃЎЧвBE+DF=EFЃЎЪдЧѓЁЯEAFЖШЪ§ЃЎ
аЁЭѕЭЌбЇЬНОПДЫЮЪЬтЕФЗНЗЈЪЧЃЌбгГЄFDЕНЕуGЃЎЪЙDG=BEЃЎСЌНсAGЃЌЯШжЄУїЁїABEЁеЁїADGЃЌдйжЄУїЁїAEFЁеЁїAGFЃЌПЩЕУЧѓГіЁЯEAFЖШЪ§ЃЌЫћЧѓГіЕФЁЯEAFЖШЪ§гІЪЧ ЃЎЧыФуИљОнЫћЕФЫМТЗЭъГЩТлжЄЙ§ГЬ.
(2)ШчЭМ2ЃЌШєдкЫФБпаЮABCDжаЃЌAB=ADЃЌЁЯB+ЁЯD=180ЁуЃЎEЃЌFЗжБ№ЪЧBCЃЌCDЩЯЕФЕуЃЌЪдЬНОПЕБЁЯEAFгыЁЯBADТњзуЪВУДЙиЯЕЪБгаBE+DF=EFЃЌВЂЫЕУїРэгЩЃЎ

ЁОД№АИЁПЃЈ1ЃЉ60ЁуЃЛЃЈ2ЃЉЕБЁЯEAFЃН![]() ЁЯBADЪБгаBE+DF=EFЃЌРэгЩМћНтЮі.
ЁЯBADЪБгаBE+DF=EFЃЌРэгЩМћНтЮі.
ЁОНтЮіЁП
ЃЈ1ЃЉбгГЄFDЕНЕуGЃЎЪЙDGЃНBEЃЎСЌНсAGЃЌМДПЩжЄУїЁїABEЁеЁїADGЃЌПЩЕУAEЃНAGЃЌдйжЄУїЁїAEFЁеЁїAGFЃЌПЩЕУЁЯEAFЃНЁЯGAFЃЌМДПЩНтЬтЃЛ
ЃЈ2ЃЉбгГЄFDЕНЕуGЃЎЪЙDGЃНBEЃЎСЌНсAGЃЌМДПЩжЄУїЁїABEЁеЁїADGЃЌПЩЕУAEЃНAGЃЌдйжЄУїЁїAEFЁеЁїAGFЃЌПЩЕУЁЯEAFЃНЁЯGAFЃЌМДПЩНтЬтЃЎ
НтЃКЃЈ1ЃЉдкЁїABEКЭЁїADGжаЃЌ ЃЌ
ЃЌ
ЁрЁїABEЁеЁїADGЃЈSASЃЉЃЌ
ЁрAEЃНAGЃЌЁЯBAEЃНЁЯDAGЃЌ
ЁпBE+DF=EFЃЌ
ЁрDG+DF=EFЃЌМДGF=EFЃЌ
дкЁїAEFКЭЁїAGFжаЃЌ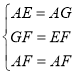 ЃЌ
ЃЌ
ЁрЁїAEFЁеЁїAGFЃЈSSSЃЉЃЌ
ЁрЁЯEAFЃНЁЯGAFЃЌ
ЁрЁЯEAFЃНЁЯFAD+ЁЯDAGЃЌМДЁЯEAFЃНЁЯFAD+ЁЯBAEЃЌ
ЁрЁЯEAFЃН![]() ЁЯBADЃН60ЁуЃЛ
ЁЯBADЃН60ЁуЃЛ
ЃЈ2ЃЉЕБЁЯEAFЃН![]() ЁЯBADЪБгаBE+DF=EFЃЌ
ЁЯBADЪБгаBE+DF=EFЃЌ
РэгЩЃКбгГЄFDЕНЕуGЃЌЪЙDGЃНBEЃЎСЌНсAGЃЌ
ЁпЁЯB+ЁЯADF=180ЁуЃЌЁЯADF+ЁЯADG=180ЁуЃЌ
ЁрЁЯB=ЁЯADGЃЌ
дкЁїABEКЭЁїADGжаЃЌ ЃЌ
ЃЌ
ЁрЁїABEЁеЁїADGЃЈSASЃЉЃЌ
ЁрAEЃНAGЃЌЁЯBAEЃНЁЯDAGЃЌ
ЁпBE+DF=EFЃЌ
ЁрDG+DF=EFЃЌМДGF=EFЃЌ
дкЁїAEFКЭЁїAGFжаЃЌ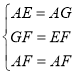 ЃЌ
ЃЌ
ЁрЁїAEFЁеЁїAGFЃЈSSSЃЉЃЌ
ЁрЁЯEAFЃНЁЯGAFЃЌ
ЁрЁЯEAFЃНЁЯFAD+ЁЯDAGЃЌМДЁЯEAFЃНЁЯFAD+ЁЯBAEЃЌ
ЁрЁЯEAFЃН![]() ЁЯBADЃЌ
ЁЯBADЃЌ
ЁрЕБЁЯEAFЃН![]() ЁЯBADЪБгаBE+DF=EF.
ЁЯBADЪБгаBE+DF=EF.


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛЖЈФмШЗЖЈЁїABCЁеЁїDEFЕФЬѕМўЪЧЃЈ ЃЉ
A.AB=DE,BC=EF,ЁЯA=ЁЯDB.ЁЯA=ЁЯE,AB=EF,ЁЯB=ЁЯD
C.ЁЯA=ЁЯD,AB=DE,ЁЯB=ЁЯED.ЁЯA=ЁЯD,ЁЯB=ЁЯE,ЁЯC=ЁЯF
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЦНУцжБНЧзјБъЯЕxOyжаЃЌХзЮяЯпy=mx2Љ2m2x+2НЛyжсгкAЕуЃЌНЛжБЯпx=4гкBЕуЃЎ
ЃЈ1ЃЉХзЮяЯпЕФЖдГЦжсЮЊx=_____ЃЈгУКЌmЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЃЈ2ЃЉШєABЁЮxжсЃЌЧѓХзЮяЯпЕФБэДяЪНЃЛ
ЃЈ3ЃЉМЧХзЮяЯпдкAЃЌBжЎМфЕФВПЗжЮЊЭМЯѓGЃЈАќКЌAЃЌBСНЕуЃЉЃЌШєЖдгкЭМЯѓGЩЯШЮвтвЛЕуPЃЈxpЃЌypЃЉЃЌypЁм2ЃЌЧѓmЕФШЁжЕЗЖЮЇЃЎ
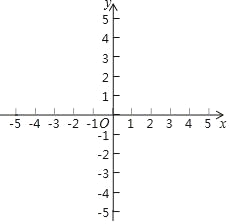
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГзЁеЌаЁЧјдкзЁеЌНЈЩшЪБСєЯТвЛПщ1798ЦНЗНУзЕФОиаЮПеЕиЃЌзМБИНЈвЛИіОиаЮЕФТЖЬьгЮгОГиЃЌЩшМЦЭМШчЭМЫљЪОЃЌгЮгОГиЕФГЄЪЧПэЕФ2БЖЃЌдкгЮгОГиЕФЧАВрСєвЛПщ5УзПэЕФПеЕиЃЌЦфЫћШ§ВрИїБЃСє2УзПэЕФЕРТЗМА1УзПэЕФТЬЛЏДјЃЎ
(1)ЧыФуМЦЫуГігЮгОГиЕФГЄКЭПэЃЛ
(2)вбжЊЬљ1ЦНЗНУзДЩзЉашЗбгУ50дЊЃЌШєгЮгОГиЩю3УзЃЌЯжвЊАбГиЕзКЭГиБк(ЙВ5ИіУц)ЖМЬљЩЯДЩзЉЃЌЙВашвЊЗбгУЖрЩйдЊЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯBACЃН30ЁуЃЌвдABЮЊжБОЖЕФЁбOОЙ§ЕуC.Й§ЕуCзїЁбOЕФЧаЯпНЛABЕФбгГЄЯпгкЕуP.ЕуDЮЊдВЩЯвЛЕуЃЌЧвBC=CD ЃЌЯвADЕФбгГЄЯпНЛЧаЯпPCгкЕуEЃЌСЌНгBCЃЎ
ЃЈ1ЃЉХаЖЯOBКЭBPЕФЪ§СПЙиЯЕ,ВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉШєЁбOЕФАыОЖЮЊ2ЃЌЧѓAEЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛжЛВЛЭИУїЕФДќзгжазАга3ИіЧђЃЌЧђЩЯЗжБ№БъгаЪ§зж0ЃЌ1ЃЌ2ЃЌетаЉЧђГ§СЫЪ§зжЭтЦфгрЖМЯрЭЌЃЌМзЁЂвдСНШЫЭцУўЧђгЮЯЗЃЌЙцдђШчЯТЃКЯШгЩМзЫцЛњУўГівЛИіЧђЃЈВЛЗХЛиЃЉЃЌдйгЩввЫцЛњУўГівЛИіЧђЃЌСНШЫУўГіЕФЧђЫљБъЕФЪ§зжжЎКЭЮЊХМЪ§ЪБдђМзЪЄЃЌКЭЮЊЦцЪ§ЪБдђввЪЄЃЎ
ЃЈ1ЃЉгУЛЪїзДЭМЛђСаБэЕФЗНЗЈСаГіЫљгаПЩФмЕФНсЙћЃЛ
ЃЈ2ЃЉетбљЕФгЮЯЗЙцдђЪЧЗёЙЋЦНЃПЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕиУцЩЯСНИіДхзЏCЁЂDДІгкЭЌвЛЫЎЦНЯпЩЯЃЌвЛЗЩааЦїдкПежавд6ЧЇУз/аЁЪБЕФЫйЖШбиMNЗНЯђЫЎЦНЗЩааЃЌКНЯпMNгыCЁЂDдкЭЌвЛЧІжБЦНУцФкЃЎЕБИУЗЩааЦїЗЩаажСДхзЏCЕФе§ЩЯЗНAДІЪБЃЌВтЕУЁЯNAD=60ЁуЃЛИУЗЩааЦїДгAДІЗЩаа40ЗжжгжСBДІЪБЃЌВтЕУЁЯABD=75ЁуЃЎЧѓДхзЏCЁЂDМфЕФОрРыЃЈ![]() ШЁ1.73ЃЌНсЙћОЋШЗЕН0.1ЧЇУзЃЉ
ШЁ1.73ЃЌНсЙћОЋШЗЕН0.1ЧЇУзЃЉ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
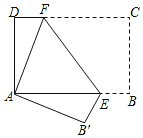
ЁОЬтФПЁПШчЭМЃЌНЋГЄЗНаЮжНЦЌABCDелЕўЃЌЪЙЕуCгыЕуAжиКЯЃЌелКлEFЗжБ№гыABЁЂDCНЛгкЕуEКЭЕуFЃЎ
ЃЈ1ЃЉЪдаДГіЭМжаШєИЩЯрЕШЕФЯпЖЮКЭШёНЧЃЈЗжБ№аДСНЖдЃЉЃЛ
ЃЈ2ЃЉжЄУїЃКЁїADFЁеЁїABЁфEЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌAB=AC=12cmЃЌBC=9cmЃЌЕуDЮЊABЕФжаЕуЃЎ

ЃЈ1ЃЉШчЙћЕуPдкЯпЖЮBCЩЯвд3РхУз/УыЕФЫйЖШгЩBЯђCЕудЫЖЏЃЌЭЌЪБЕуQдкЯпЖЮCAЩЯгЩCЕуЯђAЕудЫЖЏЃЎ
ЂйШєЕуQЕФдЫЖЏЫйЖШгыЕуPЕФдЫЖЏЫйЖШЯрЕШЃЌЕБОЙ§1УыЪБЃЌЁїBPDгыЁїCQPЪЧЗёШЋЕШЃЌЧыХаЖЯВЂЫЕУїРэгЩЃЛ
ЂкШєЕуQЕФдЫЖЏЫйЖШгыЕуPЕФдЫЖЏЫйЖШВЛЯрЕШЃЌЕБЕуQЕФдЫЖЏЫйЖШЮЊЖрЩйЪБЃЌФмЙЛЪЙЁїBPDЁеЁїCPQЃП
ЃЈ2ЃЉШєЕуQвдЂкЕФдЫЖЏЫйЖШДгЕуCГіЗЂЃЌЕуPвддРДдЫЖЏЫйЖШДгЕуBЭЌЪБГіЗЂЃЌЖМФцЪБеыбиЁїABCЕФШ§БпдЫЖЏЃЌЧѓОЙ§ЖрГЄЪБМфЃЌЕуPгыЕуQЕквЛДЮдкЁїABCЕФФФЬѕБпЩЯЛсЯргіЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com