
【题目】某住宅小区在住宅建设时留下一块1798平方米的矩形空地,准备建一个矩形的露天游泳池,设计图如图所示,游泳池的长是宽的2倍,在游泳池的前侧留一块5米宽的空地,其他三侧各保留2米宽的道路及1米宽的绿化带.
(1)请你计算出游泳池的长和宽;
(2)已知贴1平方米瓷砖需费用50元,若游泳池深3米,现要把池底和池壁(共5个面)都贴上瓷砖,共需要费用多少元?

【答案】(1)游泳池的长为50米,宽为25米;(2)共需要费用85000元.
【解析】
(1)可先设出游泳池的长和宽,然后根据条件表示出矩形空地的长和宽,然后根据矩形空地的面积是1798平方米来列方程求解.
(2)本题的关键是求出5个面的面积,有了(1)的长和宽,告诉了游泳池的高,可以用矩形的面积=长×宽计算出着5个面的面积,也就求出了贴瓷砖的面积,从而得出贴上瓷砖后共需要的费用.
解:(1)设游泳池的宽为x米,则长为2x米.
根据题意,得
(2x+2+5+1)·(x+2+2+1+1)=1798,
整理,得x2+10x-875=0,
解得x1=-35(不合题意,舍去),x2=25.
∴2x=2×25=50.
答:游泳池的长为50米,宽为25米.
(2)![]() ×50=(450+1250)×50=1700×50=85000(元).
×50=(450+1250)×50=1700×50=85000(元).
答:共需要费用85000元.


科目:初中数学 来源: 题型:
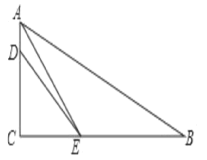
【题目】已知,如图,在Rt△ABC中,∠ACB=90°,AE平分∠BAC交BC于点E,D为AC上的点,BE=DE.
(1)求证:∠B+∠EDA=180°;
(2)求![]() 的值。.
的值。.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数y=x2+mx+1,当0<x≤2时的函数值总是非负数,则实数m的取值范围为( )
A. m≥﹣2 B. ﹣4≤m≤﹣2 C. m≥﹣4 D. m≤﹣4或m≥﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一条抛物线的对称轴是直线x=1;它与x轴相交于A,B两点(点A在点B的左边),且线段AB的长是4;它还与过点C(1,﹣2)的直线有一个交点是D(2,﹣3).
(1)求这条直线的函数解析式;
(2)求这条抛物线的函数解析式;
(3)若这条直线上有P点,使S△PAB=12,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
我们可以通过下列步骤估计![]() 的大小.
的大小.
第一步:因为12=1,22=4,1<2<4,所以1<![]() <2.
<2.
第二步:通过取1和2的平均数缩小![]() 所在的范围:取
所在的范围:取![]() ,
,
因为1.52=2.25,2<2.25,所以1<![]() <1.5.
<1.5.
(1)请仿照第一步,通过运算,确定![]() 界于哪两个相邻的整数之间?
界于哪两个相邻的整数之间?
(2)在1<![]() <1.5的基础上,重复应用第二步中取平均数的方法,将
<1.5的基础上,重复应用第二步中取平均数的方法,将![]() 所在的范围缩小至m<
所在的范围缩小至m<![]() <n,使得n-m=
<n,使得n-m=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回),商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费,某顾客刚好消费200元.
(1)该顾客至少可得到_____元购物券,至多可得到_______元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点.且BE+DF=EF.试求∠EAF度数.
小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得求出∠EAF度数,他求出的∠EAF度数应是 .请你根据他的思路完成论证过程.
(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,试探究当∠EAF与∠BAD满足什么关系时有BE+DF=EF,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.

(1)求证:AB=CF;
(2)连接DE,若AD=2AB,求证:DE⊥AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
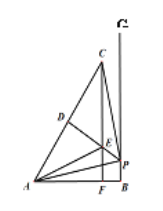
【题目】如图,线段AB=8,射线BG⊥AB,P为射线BG上一点,连接AP,作AP⊥CP且AP=CP,连接AC,PD平分∠APC,且C、D与点B在AP两侧,在线段DP取一点E,使∠EAP=∠BAP,连接CE与线段AB相交于点F(点F与点A、B不重合).
(1)求证:△AEP≌△CEP;
(2)判断CF与AB的位置关系,并说明理由;
(3)求△AEF的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com