
【题目】如图,将长方形纸片ABCD折叠,使点C与点A重合,折痕EF分别与AB、DC交于点E和点F.
(1)试写出图中若干相等的线段和锐角(分别写两对);
(2)证明:△ADF≌△AB′E.
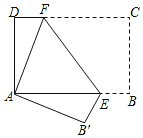
【答案】(1)∠D=∠B,∠B=∠B′;AD=CB,CB=AB′;(2)证明见解析
【解析】
(1)根据折叠的性质和矩形的性质可得答案;
(2)根据折叠的性质和矩形的性质可得∠D=∠B′=90°,AD=AB′,根据同角的余角相等可得∠DAF=∠B′AE,然后利用ASA即可证明三角形全等.
解:(1)由题意可得:∠D=∠B,∠B=∠B′;AD=CB,CB=AB′;
(2)∵四边形ABCD是长方形,
∴∠D=∠B=∠B′=90°,AD=CB=AB′,
∵∠DAF+∠EAF=90°,∠B′AE+∠EAF=90°,
∴∠DAF=∠B′AE,
在△ADF和△AB′E中,
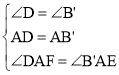 ,
,
∴△ADF≌△AB′E(ASA).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】对于二次函数y=x2+mx+1,当0<x≤2时的函数值总是非负数,则实数m的取值范围为( )
A. m≥﹣2 B. ﹣4≤m≤﹣2 C. m≥﹣4 D. m≤﹣4或m≥﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点.且BE+DF=EF.试求∠EAF度数.
小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得求出∠EAF度数,他求出的∠EAF度数应是 .请你根据他的思路完成论证过程.
(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,试探究当∠EAF与∠BAD满足什么关系时有BE+DF=EF,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.

(1)求证:AB=CF;
(2)连接DE,若AD=2AB,求证:DE⊥AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着退耕还林政策的进一步落实,三岗村从2015年底到2017年底林地面积变化如图所示,则2016,2017这两年三岗村林地面积年平均增长的百分率为( )
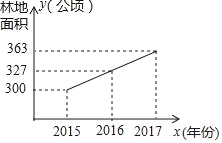
A. 7% B. 10% C. 11% D. 21%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10,BC=12,AD=8,AD是BC边上的高.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是( ).
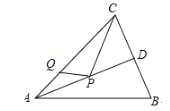
A.6B.8C.9.6D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
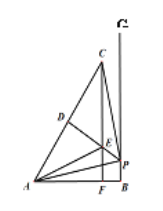
【题目】如图,线段AB=8,射线BG⊥AB,P为射线BG上一点,连接AP,作AP⊥CP且AP=CP,连接AC,PD平分∠APC,且C、D与点B在AP两侧,在线段DP取一点E,使∠EAP=∠BAP,连接CE与线段AB相交于点F(点F与点A、B不重合).
(1)求证:△AEP≌△CEP;
(2)判断CF与AB的位置关系,并说明理由;
(3)求△AEF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC中,∠A=90°,AB=AC,点D为BC的中点.
(1)如图①,若点E、F分别为AB、AC上的点,且DE⊥DF,求证:BE=AF;
(2)若点E、F分别为AB、CA延长线上的点,且DE⊥DF,那么BE=AF吗?请利用图②说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com