
【题目】如图,在△ABC中,∠BAC=30°,以AB为直径的⊙O经过点C.过点C作⊙O的切线交AB的延长线于点P.点D为圆上一点,且BC=CD ,弦AD的延长线交切线PC于点E,连接BC.
(1)判断OB和BP的数量关系,并说明理由;
(2)若⊙O的半径为2,求AE的长.

【答案】(1)OB=BP,理由见解析(2)3
【解析】
(1)由题文过C点切线,可连接OC得垂直,又根据直角三角形中30°所对的直角边等于斜边的一半,可得OB=BP.
(2)由(1)可知AP的长,且∠P=30°,若∠E=90°,则可得AE=![]() AP=3.又已知BC=CD,则∠BAD=60°,所以在△APE中∠E=90°.继而得到答案.
AP=3.又已知BC=CD,则∠BAD=60°,所以在△APE中∠E=90°.继而得到答案.
解:(1)OB=BP.

连接OC,
∵PC切⊙O于点C,∴∠OCP=90°.
∵OA=OC,∠OAC=30°,∴∠OAC=∠OCA=30°.
∴∠COP=60°.∴∠P=30°.
在Rt△OCP中,OB=OC=![]() OP= BP.
OP= BP.
(2)由(1)得OB=![]() OP.
OP.
∵⊙O的半径是2,∴AP=3OB=3×2=6.
又∵BC=CD,∴∠CAD=∠BAC=30°,∠BAD=60°.
∵∠P=30°,∴∠E=90°.
在Rt△AEP中,AE=![]() AP=
AP=![]() ×6=3.
×6=3.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中,![]() 的顶点都在网格点上,其中,C点坐标为
的顶点都在网格点上,其中,C点坐标为![]() .
.
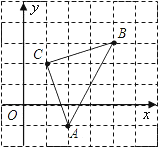
(1)写出点A、B的坐标:
![]() ______ ,______
______ ,______ ![]() 、
、![]() ______ ,______
______ ,______ ![]()
(2)将![]() 先向左平移2个单位长度,再向上平移1个单位长度,得到
先向左平移2个单位长度,再向上平移1个单位长度,得到![]() ,则
,则![]() 的三个顶点坐标分别是
的三个顶点坐标分别是![]() ______ ,______
______ ,______ ![]() 、
、![]() ______ ,______
______ ,______ ![]() 、
、![]() ______ ,______
______ ,______ ![]()
(3)求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
我们可以通过下列步骤估计![]() 的大小.
的大小.
第一步:因为12=1,22=4,1<2<4,所以1<![]() <2.
<2.
第二步:通过取1和2的平均数缩小![]() 所在的范围:取
所在的范围:取![]() ,
,
因为1.52=2.25,2<2.25,所以1<![]() <1.5.
<1.5.
(1)请仿照第一步,通过运算,确定![]() 界于哪两个相邻的整数之间?
界于哪两个相邻的整数之间?
(2)在1<![]() <1.5的基础上,重复应用第二步中取平均数的方法,将
<1.5的基础上,重复应用第二步中取平均数的方法,将![]() 所在的范围缩小至m<
所在的范围缩小至m<![]() <n,使得n-m=
<n,使得n-m=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小型企业实行工资与业绩挂钩制度,工人工资分为A、B、C、D四个档次.小明对该企业三月份工人工资进行调查,并根据收集到的数据,绘制了如下尚不完整的统计表与扇形统计图.
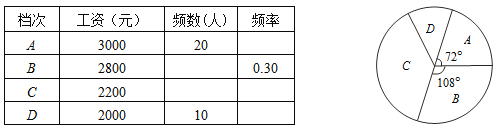
根据上面提供的信息,回答下列问题:
(1)求该企业共有多少人?
(2)请将统计表补充完整;
(3)扇形统计图中“C档次”的扇形所对的圆心角是 度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点.且BE+DF=EF.试求∠EAF度数.
小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得求出∠EAF度数,他求出的∠EAF度数应是 .请你根据他的思路完成论证过程.
(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,试探究当∠EAF与∠BAD满足什么关系时有BE+DF=EF,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为更好地开展“传统文化进校园”活动,随机抽查了部分学生,了解他们最喜爱的传统文化项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布直方图.
最喜爱的传统文化项目类型频数分布表


根据以上信息完成下列问题:
(1)直接写出频数分布表中a的值;
(2)补全频数分布直方图;
(3)若全校共有学生1500名,估计该校最喜爱围棋的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着退耕还林政策的进一步落实,三岗村从2015年底到2017年底林地面积变化如图所示,则2016,2017这两年三岗村林地面积年平均增长的百分率为( )
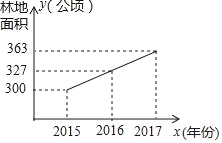
A. 7% B. 10% C. 11% D. 21%
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com