练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在△ABC中AD是∠A的外角平分线，P是AD上一动点且不与点A、D重合，记PB＋PC＝a，AB＋AC＝b，则a、b的大小关系是（ ）

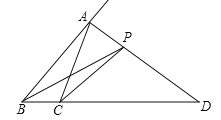
    A．a＞b B．a＝b C．a＜b D．不能确定

    【答案】A．

    【解析】

    试题分析：如图，在BA的延长线上取一点E，使AE=AC，连接EP．由AD是∠BAC的外角平分线，可知∠CAP=∠EAP，在△ACP和△AEP中，∵AE=AC，∠EAP=∠PAC，AP=AP，∴△ACP≌△AEP（SAS），∴PC=PE，在△BPE中，PB+PE＞BE，而BE=AB+AE=AB+AC，故PB+PE＞AB+AC，所以PB+PC＞AB+AC，∵PB+PC=a，AB+AC=b，∴a＞b．故选A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】把下列各式分解因式：
    （1）3x﹣12x3
    （2）（x2+4）2﹣16x2
    （3）y（y+4）﹣4（y+1）
    （4）
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线l1的最高点为P（3，4），且经过点A（0，1），将抛物线l1绕原点O旋转180°后，得到抛物线l2 ， 求l2的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】认真阅读下面关于三角形内外角平分线的研究片断，完成所提出的问题.

    探究1：如图(1)在△ABC中，O是∠ABC与∠ACB的平分线BO和CO的交点，通过分析发现∠BOC=90°+∠A，理由如下：

    ∵BO和CO分别是∠ABC和∠ACB的角平分线，∴∠1=∠ABC，∠2=∠ACB.

    ∴∠1+∠2= (∠ABC+∠ACB)= (180°－∠A)=90°－∠A.

    ∴∠BOC=180°－(∠1+∠2)=180°－(90°－∠A)=90°+∠A

    探究2：如图(2)中，O是∠ABC与外角∠ACD的平分线BO和CO的交点，试分析∠BOC与∠A有怎样的关系？请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】反比例函数y= 的图象如图，给出以下结论：
    ①常数k＜1；
    ②在每一个象限内，y随x的增大而减小；
    ③若点A（﹣1，a）和A′（1，b）都在该函数的图象上，则a+b=0；
    ④若点B（﹣2，h）、C（ ，m）、D（3，n）在该函数的图象上，则h＜m＜n．
    其中正确的结论是（ ）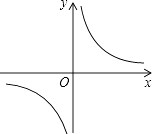

    A.①②
    B.②③
    C.③④
    D.②④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（10分）如图，△ABC中，边AB、AC的垂直平分线分别交BC于D、E．

    （1）若BC=10，则△ADE周长是多少？为什么？

    （2）若∠BAC=128°，则∠DAE的度数是多少？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】问题背景：

    如图1，在四边形ABCD中，AB＝AD，∠BAD＝120°，∠B＝∠ADC＝90°，EF分别是BC，CD上的点，且∠EAF＝60°，探究图中线段BE，EF，FD之间的数量关系.

    小王同学探究此问题的方法是延长FD到点G，使DG＝BE，连结AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是__________________；

    探索延伸：

    如图2，若在四边形ABCD中，AB＝AD，∠B＋∠D＝180°，E，F分别是BC，CD上的点，且∠EAF＝∠BAD，上述结论是否仍然成立，并说明理由；

    结论应用：

    如图3，在某次军事演习中，舰艇甲在指挥中心(O处)北偏西30°的A处，舰艇乙在指挥中心南偏东70°的B处，并且两舰艇到指挥中心的距离相等．接到行动指令后，舰艇甲向正东方向以50海里/小时的速度前进，舰艇乙沿北偏东50°的方向以60海里/小时的速度前进，1.5小时后，指挥中心观测到甲、乙两舰艇分别到达E，F处，且两舰艇与指挥中心O之间夹角∠EOF=70°，试求此时两舰艇之间的距离．

    能力提高：

    如图4，等腰直角三角形ABC中，∠BAC＝90°，AB＝AC，点M，N在边BC上，且∠MAN＝45°．若BM＝5，CN＝12，则MN的长为_________．（直接写出答案）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AD=AE，∠ADC=∠AEB，BE与CD相交于点O．

    (1)在不添加辅助线的情况下，由已知条件可以得出许多结论，例如：△ABE≌△ACD、∠DOB=∠EOC、∠DOE=∠BOC等．请你动动脑筋，再写出3个结论

    (所写结论不能与题中举例相同且只要写出3个即可)

    ① ，② ，③ ，

    (2)请你从自己写出的结论中，选取一个说明其成立的理由．

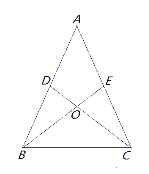
    查看答案和解析>>

    科目：初中数学 来源： 题型：

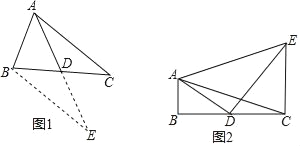
    【题目】数学兴趣小组在活动时，老师提出了这样一个问题：如图1，在△ABC中，AB=8，AC=6，D是BC的中点，求BC边上的中线AD的取值范围．

    小明在组内经过合作交流，得到了如下的解决方法：延长AD到E，使DE=AD，再证明“△ADC≌△EDB”．

    （1）探究得出AD的取值范围是_____；

    （2）（问题解决）如图2，△ABC中，∠B=90°，AB=2，AD是△ABC的中线，CE⊥BC，CE=4，且∠ADE=90°，求AE的长．

    查看答案和解析>>

    同步练习册答案