
����Ŀ�����ⱳ����
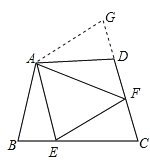
��ͼ1�����ı���ABCD�У�AB��AD����BAD��120�㣬��B����ADC��90�㣬EF�ֱ���BC��CD�ϵĵ㣬�ҡ�EAF��60����̽��ͼ���߶�BE��EF��FD֮���������ϵ.
С��ͬѧ̽��������ķ������ӳ�FD����G��ʹDG��BE������AG����֤����ABE�ա�ADG����֤����AEF�ա�AGF�����ó����ۣ����Ľ���Ӧ��__________________��
̽�����죺
��ͼ2�������ı���ABCD�У�AB��AD����B����D��180�㣬E��F�ֱ���BC��CD�ϵĵ㣬�ҡ�EAF��![]() ��BAD�����������Ƿ���Ȼ��������˵�����ɣ�
��BAD�����������Ƿ���Ȼ��������˵�����ɣ�
����Ӧ�ã�
��ͼ3����ij�ξ�����ϰ�У���ͧ����ָ������(O��)��ƫ��30����A������ͧ����ָ��������ƫ��70����B������������ͧ��ָ�����ĵľ�����ȣ��ӵ��ж�ָ���ͧ��������������50����/Сʱ���ٶ�ǰ������ͧ���ر�ƫ��50���ķ�����60����/Сʱ���ٶ�ǰ����1.5Сʱ��ָ�����Ĺ۲�ס�������ͧ�ֱ�E��F����������ͧ��ָ������O֮��нǡ�EOF=70���������ʱ����֮ͧ��ľ��룮
������ߣ�
��ͼ4������ֱ��������ABC�У���BAC��90�㣬AB��AC����M��N�ڱ�BC�ϣ��ҡ�MAN��45������BM��5��CN��12����MN�ij�Ϊ_________����ֱ��д���𰸣�




���𰸡�BE+DF=EF13
��������
��ת��⼴��.
���ⱳ����EF=BE+DF��
̽�����죺EF=BE+DF��Ȼ������
֤�����£���ͼ���ӳ�FD��G��ʹDG=BE������AG��
�ߡ�B+��ADC=180�㣬��ADC+��ADG=180�㣬
���B=��ADG��
�ڡ�ABE�͡�ADG�У�
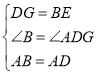 ��
��
���ABE�ա�ADG��SAS����
��AE=AG����BAE=��DAG��
�ߡ�EAF=![]() ��BAD��
��BAD��
���GAF=��DAG+��DAF=��BAE+��DAF=��BAD-��EAF=��EAF��
���EAF=��GAF��
�ڡ�AEF�͡�GAF�У�
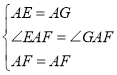 ��
��
���AEF�ա�GAF��SAS����
��EF=FG��
��FG=DG+DF=BE+DF��
��EF=BE+DF��
ʵ��Ӧ�ã���ͼ������EF���ӳ�AE��BF�ཻ�ڵ�C��

�ߡ�AOB=30��+90��+��90�㩁70�㣩=140�㣬
��EOF=70�㣬
���EAF=��AOB��
�֡�OA=OB��
��OAC+��OBC=��90�㩁30�㣩+��70��+50�㣩=180�㣬
�����̽�������е�������
�����EF=AE+BF������
��EF=1.5����50+60��=165���
�𣺴�ʱ����֮ͧ��ľ�����165���
������ߣ�MN=13.


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(8��)��һ�ų�����ֽ��ABCD����ͼ��ʾ�۵������۵��ǡ�FEC��64��.
(1)���1�Ķ�����
(2)��֤����EFG�ǵ��������Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB�ǡ�O��ֱ������ǡ�DAB��ƽ����AC����O�ڵ�C����CD��AD������ΪD��ֱ��CD��AB���ӳ��߽��ڵ�E�� 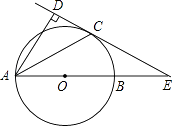
��1����֤��ֱ��CDΪ��O�����ߣ�
��2����AB=2BE����CE= ![]() ʱ����AD�ij���
ʱ����AD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC��AD����A�����ƽ���ߣ�P��AD��һ�����Ҳ����A��D�غϣ���PB��PC��a��AB��AC��b����a��b�Ĵ�С��ϵ�ǣ� ��
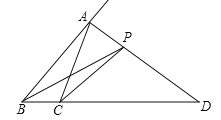
A��a��b B��a��b C��a��b D������ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ijסլС����ʩ��������������һ��յأ���֪AD=8�ף�CD=6�ף���ADC=90�㣬AB=26�ף�BC=24�ף�С��Ϊ�������������ڿյ����̲�ƺ����֪��ƺÿƽ����100Ԫ�������øò�ƺ�������յع��軨�Ѷ���Ԫ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC��DE�۵�������A�����ı���BCDE�ڲ�ʱ����A����1+��2֮����һ��������ϵʼ�ձ��ֲ��䣬��������һ��������ɣ��㷢�ֵĹ�����ʲô����˵�����ҳ��Ĺ��ɵ���ȷ�ԣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ������ABC����ADE�У���BAC=��DAE=90�㣬AB=AC��AD=AE����C��D��E������ͬһֱ���ϣ�����BD��
��1����֤����BAD�ա�CAE��
��2���Բ���BD��CE�к�����λ�ù�ϵ����֤����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=��x2+mx��m��0��m��1����x�ύ��ԭ��O�͵�A����B������Ϊ��1����1��������AB�����߶�AB�Ƶ�A˳ʱ����ת90��õ��߶�AC������OB��OC��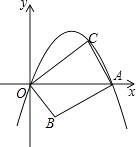
��1�����A�ĺ����꣮���ú�m�Ĵ���ʽ��ʾ����
��2����m=3�����C������Ϊ ��
��3������C�������ߵĶ����غ�ʱ�����ı���ABOC�������
��4�����m��ȡֵ��Χ��ֱ��д����AOC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ȫ�ȵĵ���ֱ�����ǰ壨ֱ�DZ߳�Ϊ4��������һ�������ǰ�EFG��ֱ�Ƕ���Gλ�����ǰ�ABC��б���е㴦���ֽ����ǰ�EFG��G�㰴˳ʱ�뷽����ת���ȣ�0�㣼����90�㣩����ͼ1�����ı���GKCHΪ�����ǰ���ص����֣�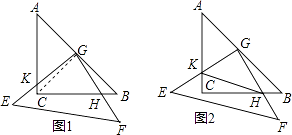
��1������BH��CK��������������ϵ����֤����Ľ��ۣ�
��2������HK����ͼ2������������ת�����У���BH=x����GKH�����Ϊy��
����y��x֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
�ڵ���GKH�����ǡ�õ��ڡ�ABC����� ![]() ����x��
����x��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com