
【题目】先阅读下列材料,然后解决后面的问题.
材料:一个三位数![]() (百位数为a,十位数为b,个位数为c),若a+c=b,则称这个三整数
(百位数为a,十位数为b,个位数为c),若a+c=b,则称这个三整数![]() 为“协和数”,同时规定c=
为“协和数”,同时规定c=![]() (k≠0),k称为“协和系数”,如264,因为它的百位上数字2与个位数字4之和等于十位上的数字6,所有264是“协和数”,则“协和数”k=2×4=8.
(k≠0),k称为“协和系数”,如264,因为它的百位上数字2与个位数字4之和等于十位上的数字6,所有264是“协和数”,则“协和数”k=2×4=8.
(1)对于“协和数”![]() ,求证:“协和数”
,求证:“协和数”![]() 能被11整除.
能被11整除.
(2)已知有两个十位数相同的“协和数”![]() ,
,![]() (a1>a2),且k1﹣k2=1,若y=k1+k2,用含b的式子表示y.
(a1>a2),且k1﹣k2=1,若y=k1+k2,用含b的式子表示y.
【答案】(1)证明见解析;(2)y==![]() ﹣1.
﹣1.
【解析】
(1)根据协和数的定义可得出a+c=b,由![]() =100a+10b+c可得出
=100a+10b+c可得出![]() =99a+11b,可证出“协和数
=99a+11b,可证出“协和数![]() ”能被11整除;
”能被11整除;
(2)由已知可得k1﹣k2=a1b1﹣a2b2=a1(b﹣a1)﹣a2(b﹣a2)=(a1﹣a2)(b﹣a1﹣a2)=1,a1、a2、b均为整数,故a1﹣a2=1,b﹣a1﹣a2=1,可得a1+a2=b﹣1,所以a12﹣2a1a2+a22=1①,a12+2a1a2+a22=(b﹣1)2②,由①+②得:![]() =
=![]() ,所以
,所以
y=k1+k2=a1b1+a2b2=a1(b﹣a1)+a2(b﹣a2)=b(a1+a2)﹣(![]() )=b(b﹣1)﹣
)=b(b﹣1)﹣![]() .
.
(1)证明:∵![]() 为“协和数”,
为“协和数”,
∴a+c=b,
∵![]() =100a+10b+c=99a+10b+a+c=99a+11b=11(9a+b),
=100a+10b+c=99a+10b+a+c=99a+11b=11(9a+b),
∵a是整数,b是整数,
∴9a+b是整数,
∴“协和数”![]() 能被11整除;
能被11整除;
(2)∵k1﹣k2=a1b1﹣a2b2=a1(b﹣a1)﹣a2(b﹣a2)=(a1﹣a2)(b﹣a1﹣a2)=1,a1、a2、b均为整数,
∴a1﹣a2=1,b﹣a1﹣a2=1,
∴a1+a2=b﹣1,
∴a12﹣2a1a2+a22=1①,a12+2a1a2+a22=(b﹣1)2②,
①+②得:![]() =
=![]() ,/p>
,/p>
y=k1+k2=a1b1+a2b2=a1(b﹣a1)+a2(b﹣a2)=![]() +
+![]() =b(a1+a2)﹣(
=b(a1+a2)﹣(![]() )=b(b﹣1)﹣
)=b(b﹣1)﹣![]() =
=![]() ﹣1.
﹣1.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
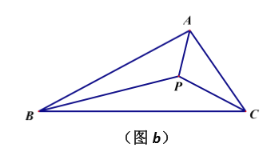
【题目】已知![]() 中,记
中,记![]() ,
,![]() .
.
(1)如图![]() ,若
,若![]() 平分
平分![]() ,
,![]() 、
、![]() 分别是
分别是![]() 的外角
的外角![]() 和
和![]() 的平分线,
的平分线,![]() ,用含
,用含![]() 的代数式表示
的代数式表示![]() 的度数,用含
的度数,用含![]() 的代数式表示
的代数式表示![]() 的度数,并说明理由.
的度数,并说明理由.

(2)如图![]() ,若点
,若点 ![]() 为
为![]() 的三条内角平分线的交点,
的三条内角平分线的交点,![]() 于点
于点 ![]() , 猜想(1)中的两个结论是否发生变化,补全图形并直接写出你的结论.
, 猜想(1)中的两个结论是否发生变化,补全图形并直接写出你的结论.
![]() .
.
![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,∠ACB=45°,点E在对角线AC上,BE=BA,BF⊥AC于点F,BF的延长线交AD于点G.点H在BC的延长线上,且CH=AG,连接EH.
(1)若BC=12![]() ,AB=13,求AF的长;
,AB=13,求AF的长;
(2)求证:EB=EH.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=4,∠BAC=90°,点D在边AB上,BE∥CD,AE⊥CD,垂足为F,且EF=2,点G在线段CF上,若∠GAF=45°,则△ACG的面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若点![]() 在数轴上分别表示实数
在数轴上分别表示实数![]() ,则
,则![]() 两点之间的距离表示为
两点之间的距离表示为![]() ,回答下列问题:
,回答下列问题:
(1)数轴上表示2和5的点之间的距离是_________;数轴上表示1和![]() 的两点之间的距离是___________;
的两点之间的距离是___________;
(2)数轴上表示![]() 和
和![]() 的两点
的两点![]() 和
和![]() 之间的距离是_______;如果
之间的距离是_______;如果![]() ,那么
,那么![]() ______;
______;
(3)![]() 的最小值为_______,相应
的最小值为_______,相应![]() 的取值范围是___________;
的取值范围是___________;
(4)已知![]() ,则
,则![]() 的最大值为_______,最小值为________.
的最大值为_______,最小值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】锐锐参加我市电视台组织的“牡丹杯”智力竞答节目,答对最后两道单选题就顺利通关,第一道单选题有3个选项,第二道单选题有4个选项,这两道题锐锐都不会,不过锐锐还有两个“求助”可以用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项).
(1)如果锐锐两次“求助”都在第一道题中使用,那么锐锐通关的概率是________;
(2)如果锐锐两次“求助”都在第二道题中使用,那么锐锐通关的概率是________;
(3)如果锐锐每道题各用一次“求助”,请用树状图或者列表来分析他顺利通关的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小型企业实行工资与业绩挂钩制度,工人工资分为A、B、C、D四个档次.小明对该企业三月份工人工资进行调查,并根据收集到的数据,绘制了如下尚不完整的统计表与扇形统计图.
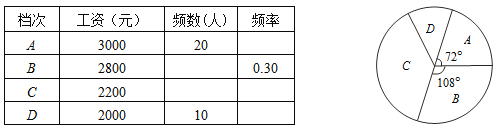
根据上面提供的信息,回答下列问题:
(1)求该企业共有多少人?
(2)请将统计表补充完整;
(3)扇形统计图中“C档次”的扇形所对的圆心角是 度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com