
【题目】若点![]() 在数轴上分别表示实数
在数轴上分别表示实数![]() ,则
,则![]() 两点之间的距离表示为
两点之间的距离表示为![]() ,回答下列问题:
,回答下列问题:
(1)数轴上表示2和5的点之间的距离是_________;数轴上表示1和![]() 的两点之间的距离是___________;
的两点之间的距离是___________;
(2)数轴上表示![]() 和
和![]() 的两点
的两点![]() 和
和![]() 之间的距离是_______;如果
之间的距离是_______;如果![]() ,那么
,那么![]() ______;
______;
(3)![]() 的最小值为_______,相应
的最小值为_______,相应![]() 的取值范围是___________;
的取值范围是___________;
(4)已知![]() ,则
,则![]() 的最大值为_______,最小值为________.
的最大值为_______,最小值为________.
【答案】(1)3,4;(2)|x+1|,1或-3;(3)3,-1≤x≤2;(4)6,-3.
【解析】
(1)根据数轴上两点间的距离的表示方法分别解答即可;
(2)根据两点间的距离的表示方法列式,再根据绝对值的性质求解即可;
(3)由|x+1|+|x-2|表示到-1和2的距离的和最小的值,即可求解;
(4)已知条件变形为|x+2|+|x-1|+|y-5|+|y+1=9|,由|x+2|+|x-1|表示到-2和1的距离的和最小的值,最小值为3,此时-2≤x≤1,|y-5|+|y+1|表示到5和-1的距离的和最小的值,最小值为6,此时-1≤y≤5,进而求解即可.
(1)数轴上表示2和5的两点之间的距离是|5-2|=3,
数轴上表示1和-3的两点之间的距离是|-3-1|=4.
故答案为3,4;
(2)数轴上表示x和-1的两点A和B之间的距离是|x+1|,
如果|AB|=2,则|x+1|=2,
所以,x+1=2或x+1=-2,
解得x=1或x=-3.
故答案为|x+1|,1或-3;
(3)因为|x+1|+|x-2|表示到-1和2的距离的最小值,所以最小值是|2-(-1)|=3,
|x+1|+|x-2|取最小值时,相应x的取值范围是-1≤x≤2.
故答案为:3,-1≤x≤2;
(4)∵|x+2|+|x-1|=9-|y-5|-|y+1|,
∴|x+2|+|x-1|+|y-5|+|y+1|=9,
∴-2≤x≤1,-1≤y≤5,
∴x+y的最大值为1+5=6,最小值为-2-1=-3.
故答案为6,-3.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④FH=![]() BD
BD
其中正确结论的为______(请将所有正确的序号都填上).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题
某校七年级一班的部分同学和二班的部分同学在元旦期间租小巴车从泸州去成都熊猫繁殖基地看熊猫宝宝,出发地到目的地约![]() ,一班的车速为
,一班的车速为![]() ,二班的车速为
,二班的车速为![]() .
.
(1)生活委员先去超市买大家都喜欢吃的零食“呀!土豆”,但超市的存货不多了,如果每人![]() 包,则剩余
包,则剩余![]() 包:如果每人
包:如果每人![]() 包,则还缺
包,则还缺![]() 包,他们一共有多少人?
包,他们一共有多少人?
(2)因为一班的某同学临时出了些状况,二班的车先走![]() ,一班的车能在到达目的地之前追上二班的车吗?如果能,什么时候追上?
,一班的车能在到达目的地之前追上二班的车吗?如果能,什么时候追上?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数分别填入相应的集合里:
![]() ,2.525525552…(相邻两个2之间的5的个数逐个加1),0,
,2.525525552…(相邻两个2之间的5的个数逐个加1),0,![]() ,
,![]() ,0.12,
,0.12,![]() ,
,![]() ,
,![]() ,
,![]()
(1)负数集合:{ …};
(2)非负整数集合:{ …};
(3)分数集合:{ …};
(4)无理数集合:{ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是一次函数y=﹣![]() x+
x+![]() 的图象与反比例函数y=
的图象与反比例函数y=![]() (m>0)的图象的一个交点,AB⊥x轴,垂足为B,且AB=
(m>0)的图象的一个交点,AB⊥x轴,垂足为B,且AB=![]() .
.
(1)求这个反比例函数的解析式;
(2)当1<x<4,求反比例函数y=![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列材料,然后解决后面的问题.
材料:一个三位数![]() (百位数为a,十位数为b,个位数为c),若a+c=b,则称这个三整数
(百位数为a,十位数为b,个位数为c),若a+c=b,则称这个三整数![]() 为“协和数”,同时规定c=
为“协和数”,同时规定c=![]() (k≠0),k称为“协和系数”,如264,因为它的百位上数字2与个位数字4之和等于十位上的数字6,所有264是“协和数”,则“协和数”k=2×4=8.
(k≠0),k称为“协和系数”,如264,因为它的百位上数字2与个位数字4之和等于十位上的数字6,所有264是“协和数”,则“协和数”k=2×4=8.
(1)对于“协和数”![]() ,求证:“协和数”
,求证:“协和数”![]() 能被11整除.
能被11整除.
(2)已知有两个十位数相同的“协和数”![]() ,
,![]() (a1>a2),且k1﹣k2=1,若y=k1+k2,用含b的式子表示y.
(a1>a2),且k1﹣k2=1,若y=k1+k2,用含b的式子表示y.
查看答案和解析>>
科目:初中数学 来源: 题型:
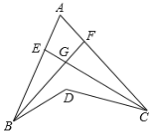
【题目】如图,BF 是∠ABD 的平分线,CE 是∠ACD 的平分线,BF 与 CE 交于 G,若∠BDC=130°,∠BGC=100°,则∠A 的度数为( )
A.60°B.70°C.80°D.90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线AB∥CD,点M,N分别在直线AB,CD上,点E为平面内一点.
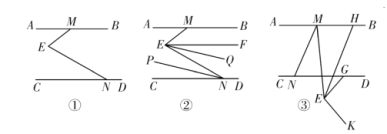
(1)如图①,探究∠AME,∠MEN,∠ENC的数量关系,并说明理由;
(2)如图②,∠AME=30°,EF平分∠MEN,NP平分∠ENC,EQ∥NP,求∠FEQ的度数;
(3)如图③,点G为CD上一点,∠AMN=m∠EMN,∠GEK=m∠GEM,EH∥MN交AB于点H,直接写出∠GEK,∠BMN,∠GEH之间的数量关系(用含m的式子表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com