
【题目】直线AB∥CD,点M,N分别在直线AB,CD上,点E为平面内一点.
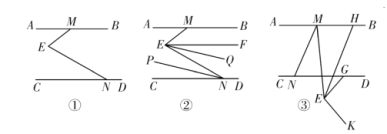
(1)如图①,探究∠AME,∠MEN,∠ENC的数量关系,并说明理由;
(2)如图②,∠AME=30°,EF平分∠MEN,NP平分∠ENC,EQ∥NP,求∠FEQ的度数;
(3)如图③,点G为CD上一点,∠AMN=m∠EMN,∠GEK=m∠GEM,EH∥MN交AB于点H,直接写出∠GEK,∠BMN,∠GEH之间的数量关系(用含m的式子表示).
【答案】(1)∠MEN=∠AME+∠ENC,见解析;(2)∠FEQ=15°;(3)∠BMN+∠GEK-m∠GEH=180°.
【解析】
(1)过点E作l∥AB,利用平行线的性质可得∠1=∠BME,∠2=∠DNE,由∠MEN=∠1+∠2,等量代换可得结论;
(2)利用角平分线的性质可得∠NEF=![]() ∠MEN,∠ENP=
∠MEN,∠ENP=![]() ∠END,由EQ∥NP,可得∠QEN=∠ENP=
∠END,由EQ∥NP,可得∠QEN=∠ENP=![]() ∠ENC,由(1)的结论可得∠MEN=∠AME+∠ENC,等量代换得出结论;
∠ENC,由(1)的结论可得∠MEN=∠AME+∠ENC,等量代换得出结论;
(3)由已知可得∠EMN=![]() ∠BMN,∠GEN=
∠BMN,∠GEN=![]() ∠GEK,由EH∥MN,可得∠HEM=∠ENM=
∠GEK,由EH∥MN,可得∠HEM=∠ENM=
![]() ∠AMN,因为∠GEH=∠GEM-∠HEM,等量代换得出结论.
∠AMN,因为∠GEH=∠GEM-∠HEM,等量代换得出结论.
解:(1)过点E作l∥AB,
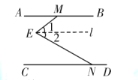
∵AB∥CD,∴l∥AB∥CD
∴∠1=∠AME,∠2=∠CNE.
∵∠MEN=∠1+∠2,
∴∠MEN=∠AME+∠ENC;
(2)∵EF平分∠MEN,NP平分∠ENC,
∴∠NEF=![]() ∠MEN,∠ENP=
∠MEN,∠ENP=![]() ∠ENC.
∠ENC.
∵EQ∥NP,∴∠QEN=∠ENP=![]() ∠ENC.
∠ENC.
由(1)可得∠MEN=∠AME+∠ENC,∴∠MEN-∠ENC=∠AME=30°.
∴∠FEQ=∠NEF-∠NEQ=![]() (∠MEN-∠ENC)=
(∠MEN-∠ENC)=![]() ×30°=15°;
×30°=15°;
(3)∠BMN+∠GEK-m∠GEH=180°.理由如下:
∵∠AMN=m∠EMN,∠GEK=m∠GEM,
∴∠EMN=![]() ∠AMN,∠GEM=
∠AMN,∠GEM=![]() ∠GEK.
∠GEK.
∵EH∥MN,∴∠HEM=∠EMN=![]() ∠AMN.
∠AMN.
∵∠GEH=∠GEM-∠HEM=![]() ∠GEK-
∠GEK-![]() ∠AMN,
∠AMN,
∴m∠GEH=∠GEK-∠AMN.
∵∠BMN+∠AMN=180°,
∴∠BMN+∠GEK-m∠GEH=180°.


科目:初中数学 来源: 题型:
【题目】若点![]() 在数轴上分别表示实数
在数轴上分别表示实数![]() ,则
,则![]() 两点之间的距离表示为
两点之间的距离表示为![]() ,回答下列问题:
,回答下列问题:
(1)数轴上表示2和5的点之间的距离是_________;数轴上表示1和![]() 的两点之间的距离是___________;
的两点之间的距离是___________;
(2)数轴上表示![]() 和
和![]() 的两点
的两点![]() 和
和![]() 之间的距离是_______;如果
之间的距离是_______;如果![]() ,那么
,那么![]() ______;
______;
(3)![]() 的最小值为_______,相应
的最小值为_______,相应![]() 的取值范围是___________;
的取值范围是___________;
(4)已知![]() ,则
,则![]() 的最大值为_______,最小值为________.
的最大值为_______,最小值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
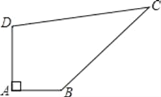
【题目】已知某开发区有一块四边形的空地ABCD,如图所示,现计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问要多少投入?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有![]() 、
、![]() 、
、![]() 三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )
三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )

A.在∠A、∠B两内角平分线的交点处
B.在AC、BC两边垂直平分线的交点处
C.在AC、BC两边高线的交点处
D.在AC、BC两边中线的交点处
查看答案和解析>>
科目:初中数学 来源: 题型:
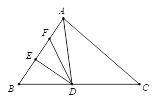
【题目】如图,△ABC中,AD平分∠BAC,DE⊥AB于点E且AE=8cm,F为AE的中点,G从A点向C点以每秒1个单位的速度运动,则点G经过_______秒时DG=DF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小型企业实行工资与业绩挂钩制度,工人工资分为A、B、C、D四个档次.小明对该企业三月份工人工资进行调查,并根据收集到的数据,绘制了如下尚不完整的统计表与扇形统计图.
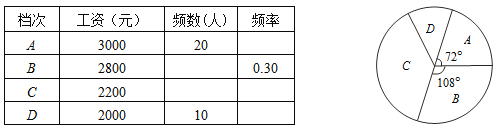
根据上面提供的信息,回答下列问题:
(1)求该企业共有多少人?
(2)请将统计表补充完整;
(3)扇形统计图中“C档次”的扇形所对的圆心角是 度.
查看答案和解析>>
科目:初中数学 来源: 题型:
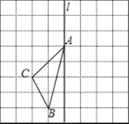
【题目】如图,在长度为1个单位长度的小正方形组成的正方形中,点A、B、C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线l成轴对称的△AB′C′;
(2)△ABC的面积为 ;
(3)以AC为边作与△ABC全等的三角形,则可作出 个三角形与△ABC全等;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠AOB内一点P,P1,P2分别P是关于OA、OB的对称点,P1P2交OA于M,交OB于N,若P1P2=6cm,则△PMN的周长是( )
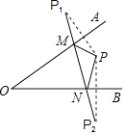
A.3cmB.4cmC.5cmD.6cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(x﹣3)(x﹣2)=|m|.
(1)求证:对于任意实数m,方程总有两个不相等的实数根;
(2)若方程的一个根是1,求m的值及方程的另一个根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com