
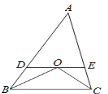
【题目】如图,在△ABC中,∠B与∠C的平分线交于点O,过点O作DE∥BC,分别交AB,AC于点D,E.若AB=5,AC=4,则△ADE的周长是______
科目:初中数学 来源: 题型:
【题目】某公园有一个抛物线形状的观景拱桥ABC,其横截面如图所示,在图中建立的直角坐标系中,抛物线的解析式为y=﹣![]() +c且过顶点C(0,5)(长度单位:m)
+c且过顶点C(0,5)(长度单位:m)
(1)直接写出c的值;
(2)现因搞庆典活动,计划沿拱桥的台阶表面铺设一条宽度为1.5m的地毯,地毯的价格为20元/m2,求购买地毯需多少元?
(3)在拱桥加固维修时,搭建的“脚手架”为矩形EFGH(H、G分别在抛物线的左右侧上),并铺设斜面EG.已知矩形EFGH的周长为27.5m,求斜面EG的倾斜角∠GEF的度数.(精确到0.1°)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1(注:与图2完全相同),二次函数y=![]() x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.
x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.
(1)求该二次函数的解析式;
(2)设该抛物线的顶点为D,求△ACD的面积;
(3)若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动,当P,Q运动到t秒时,△APQ沿PQ所在的直线翻折,点A恰好落在抛物线上E点处,请直接判定此时四边形APEQ的形状,并求出E点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形AOCB的顶点A(m,n)和C(p,q)在坐标轴上,已知![]() 和
和![]() 都是方程x+2y=4的整数解,点B在第一象限内.
都是方程x+2y=4的整数解,点B在第一象限内.
(1)求点B的坐标;
(2)若点P从点A出发沿y轴负半轴方向以1个单位每秒的速度运动,同时点Q从点C出发,沿x轴负半轴方向以2个单位每秒的速度运动,问运动到多少秒时,四边形BPOQ面积为长方形ABCO面积的一半;
(3)如图2,将线段AC沿x轴正方向平移得到线段BD,点E(a,b)为线段BD上任意一点,试问a+2b的值是否变化?若变化,求其范围;若不变化,求其值.(直接写出结论)

查看答案和解析>>
科目:初中数学 来源: 题型:
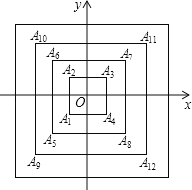
【题目】如图,所有正方形的中心都在原点,且各边也都与x轴或y轴平行,从内向外,它们的边长依次为2,4,6,8,…顶点依次用A1、A2、A3、A4表示,则顶点A2020的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ACDE是证明勾股定理时用到的一个图形,a、b、c是Rt△ABC和Rt△BED边长,易知AE=![]() c,这时我们把关于x的形如ax+
c,这时我们把关于x的形如ax+![]() cx+b=0的一元二次方程称为“勾系一元二次方程”.
cx+b=0的一元二次方程称为“勾系一元二次方程”.

请解决下列问题:
写出一个“勾系一元二次方程”;
求证:关于x的“勾系一元二次方程”ax+![]() cx+b=0必有实数根;
cx+b=0必有实数根;
若x=1是“勾系一元二次方程”ax+![]() cx+b=0的一个根,且四边形ACDE的周长是
cx+b=0的一个根,且四边形ACDE的周长是![]() ,求△ABC面积.
,求△ABC面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末小丽从家里出发骑单车去公园,因为她家与公园之间是一条笔直的自行车道,所以小丽骑得特别放松.途中,她在路边的便利店挑选一瓶矿泉水,耽误了一段时间后继续骑行,愉快地到了公园.图中描述了小丽路上的情景,下列说法中错误的是( )
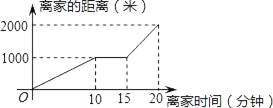
A.小丽在便利店时间为15分钟
B.公园离小丽家的距离为2000米
C.小丽从家到达公园共用时间20分钟
D.小丽从家到便利店的平均速度为100米/分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(11分)如图,边长为8的正方形OABC的两边在坐标轴上,以点C为顶点的抛物线经过点A,点P是抛物线上点A、C间的一个动点(含端点),过点P作PF⊥BC于点F. 点D、E的坐标分别为(0,6),(-4,0),连接PD,PE,DE.

(1)请直接写出抛物线的解析式;
(2)小明探究点P的位置发现:当点P与点A或点C重合时,PD与PF的差为定值. 进而猜想:对于任意一点P,PD与PF的差为定值. 请你判断该猜想是否正确,并说明理由;
(3)小明进一步探究得出结论:若将“使△PDE的面积为整数”的点P记作“好点”,则存在多个“好点”,且使△PDE的周长最小的点P也是一个“好点”.请直接写出所有“好点”的个数,并求出△PDE的周长最小时“好点”的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
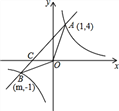
【题目】已知,如图,反比例函数y=![]() 的图象与一次函数y=x+b的图象交于点A(1,4),点B(m,-1),
的图象与一次函数y=x+b的图象交于点A(1,4),点B(m,-1),
(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出不等式x+b>![]() 的解.
的解.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com