
【题目】如图,四边形ACDE是证明勾股定理时用到的一个图形,a、b、c是Rt△ABC和Rt△BED边长,易知AE=![]() c,这时我们把关于x的形如ax+
c,这时我们把关于x的形如ax+![]() cx+b=0的一元二次方程称为“勾系一元二次方程”.
cx+b=0的一元二次方程称为“勾系一元二次方程”.

请解决下列问题:
写出一个“勾系一元二次方程”;
求证:关于x的“勾系一元二次方程”ax+![]() cx+b=0必有实数根;
cx+b=0必有实数根;
若x=1是“勾系一元二次方程”ax+![]() cx+b=0的一个根,且四边形ACDE的周长是
cx+b=0的一个根,且四边形ACDE的周长是![]() ,求△ABC面积.
,求△ABC面积.
【答案】详见解析.
【解析】试题分析:(1)直接找一组勾股数代入方程即可;
(2)通过判断根的判别式△的正负来证明结论;
(3)利用根的意义和勾股定理作为相等关系先求得c的值,根据完全平方公式求得ab的值,从而可求得面积.
试题解析:
(1)解:令a=3,b=4则c=5,写出一个“勾系一元二次方程”:3x+5![]() x+4=0;
x+4=0;
(2)证明:
∵△=(![]() c)4ab=2c4ab=2(a+b)4ab=2(a2ab+b)=2(ab)≥0,
c)4ab=2c4ab=2(a+b)4ab=2(a2ab+b)=2(ab)≥0,
∴关于x的“勾系一元二次方程”ax+![]() cx+b=0必有实数根;
cx+b=0必有实数根;
(3)代入x=1得a![]() c+b=0,∴a+b=
c+b=0,∴a+b=![]() c.
c.
由四边形ACDE的周长是![]() 得a+b+a+b+
得a+b+a+b+![]() c=
c=![]() ,
,
∴2(a+b)+![]() c=
c=![]() ,2
,2![]() c+
c+![]() c=
c=![]() ,3
,3![]() c=
c=![]() ,c=2,a+b=2
,c=2,a+b=2![]() ,
,
∴2ab=(a+b)(a+b)=(a+b)(c)=84=4,
∴ab=2,
∴△ABC面积=![]() ab=1.
ab=1.


科目:初中数学 来源: 题型:
【题目】某种型号油电混合动力汽车,从A地到B地燃油行驶纯燃油费用76元,从A地到B地用电行驶纯电费用26元,已知每行驶1千米,纯燃油费用比纯用电费用多0.5元.
(1)求每行驶1千米纯用电的费用;
(2)若要使从A地到B地油电混合行驶所需的油、电费用合计不超过39元,则至少用电行驶多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次男子马拉松长跑比赛中,随机抽得12名选手所用的时间(单位:分钟)得到如下样本数据:140 146 143 175 125 164 134 155 152 168 162 148
(1)计算该样本数据的中位数和平均数;
(2)如果一名选手的成绩是147分钟,请你依据样本数据的中位数,推断他的成绩如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知正方形的边长为4,甲、乙两动点分别从正方形ABCD的顶点A、C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行,若乙的速度是甲的速度的3倍,则它们第2017次相遇在边( )上.

A. AB B. BC C. CD D. DA
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上两点之向的距离两数差的绝对值,我们可以用表示这两个点的大写字母一起标记,比如,表示点A的数为2,点B表示的数为﹣3,点A与点B之间的距离记作AB,别AB=2﹣(﹣3)=5.
(1)数轴上表示﹣3和5的两点之间的距离是
(2)如图,在数轴上点A表示数a,点C表示数c,且|a+20|+(c﹣30)2=0.求点A与点C之间的距离AC;
(3)在(2)的条件下,在数轴上是否存在点B,使AB=5,若存在,求出点B表示的数b;若不存在,请说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
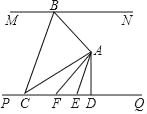
【题目】如图,直线MN∥PQ,点A在直线MN与PQ之间,点B在直线MN上,连结AB.∠ABM的平分线BC交PQ于点C,连结AC,过点A作AD⊥PQ交PQ于点D,作AF⊥AB交PQ于点F,AE平分∠DAF交PQ于点E,若∠CAE=45°,∠ACB=![]() ∠DAE,则∠ACD的度数是_____.
∠DAE,则∠ACD的度数是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学团委会为了解该校学生的课余活动情况,采取抽样的办法,从阅读、运动、娱乐、其它等四个方面调查了若干名学生的兴趣爱好,并将调查结果绘制了如下的两幅不完整的统计图(如图),请你根据图中提供的信息解答下列问题:
(1)这次抽样中,一共调查了多少名学生?
(2)“其它”在扇形图中所占的圆心角是多少度?
(3)若该校有2500名学生,你估计全校可能有多少名学生爱好阅读?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com