
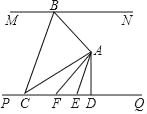
【题目】如图,直线MN∥PQ,点A在直线MN与PQ之间,点B在直线MN上,连结AB.∠ABM的平分线BC交PQ于点C,连结AC,过点A作AD⊥PQ交PQ于点D,作AF⊥AB交PQ于点F,AE平分∠DAF交PQ于点E,若∠CAE=45°,∠ACB=![]() ∠DAE,则∠ACD的度数是_____.
∠DAE,则∠ACD的度数是_____.
【答案】27°.
【解析】
延长FA与直线MN交于点K,通过角度的不断转换解得∠BCA=45°.
解:延长FA与直线MN交于点K,
由图可知∠ACD=90°-∠CAD=90°-(45°+∠EAD)=45°-![]() ∠FAD=45°-
∠FAD=45°-![]() (90°-∠AFD)=
(90°-∠AFD)=![]() ∠AFD,
∠AFD,
因为MN∥PQ,所以∠AFD=∠BKA=90°-∠KBA=90°-(180°-∠ABM)=∠ABM-90°,
所以∠ACD=![]() ∠AFD=
∠AFD=![]() (∠ABM-90°)=∠BCD-45°,即∠BCD-∠ACD=∠BCA=45°,
(∠ABM-90°)=∠BCD-45°,即∠BCD-∠ACD=∠BCA=45°,
所以∠ACD=90°-(45°+∠EAD)=45°-∠EAD=45°-![]() ∠BCA=45°-18°=27°.
∠BCA=45°-18°=27°.
故∠ACD的度数是:27°.


 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:
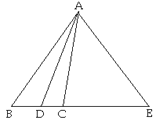
【题目】如图,AD平分∠BAC,∠EAD=∠EDA.
(1)∠EAC与∠B相等吗?为什么?
(2)若∠B=50°,∠CAD︰∠E=1︰3,求∠E的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,AC与BD相交于点O,连接CD
(1)求∠AOD的度数;
(2)求证:四边形ABCD是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ACDE是证明勾股定理时用到的一个图形,a、b、c是Rt△ABC和Rt△BED边长,易知AE=![]() c,这时我们把关于x的形如ax+
c,这时我们把关于x的形如ax+![]() cx+b=0的一元二次方程称为“勾系一元二次方程”.
cx+b=0的一元二次方程称为“勾系一元二次方程”.

请解决下列问题:
写出一个“勾系一元二次方程”;
求证:关于x的“勾系一元二次方程”ax+![]() cx+b=0必有实数根;
cx+b=0必有实数根;
若x=1是“勾系一元二次方程”ax+![]() cx+b=0的一个根,且四边形ACDE的周长是
cx+b=0的一个根,且四边形ACDE的周长是![]() ,求△ABC面积.
,求△ABC面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个装有进水管和出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,接着关闭进水管直到容器内的水放完,每分钟的进水量和出水量是两个常数,容器内的水量y(单位:L)与时间(单价:min)之间的关系如图所示。在第_______分钟时该容器内的水恰好为10L.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九(3)班为了组队参加学校举行的“五水共治”知识竞赛,在班里选取了若干名学生,分成人数相同的甲、乙两组,进行了四次“五水共治”模拟竞赛,成绩优秀的人数和优秀率分别绘制成如图统计图. 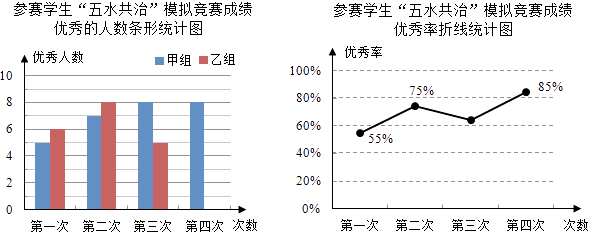
根据统计图,解答下列问题:
(1)第三次成绩的优秀率是多少?并将条形统计图补充完整;
(2)已求得甲组成绩优秀人数的平均数 ![]() =7,方差
=7,方差 ![]() =1.5,请通过计算说明,哪一组成绩优秀的人数较稳定?
=1.5,请通过计算说明,哪一组成绩优秀的人数较稳定?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O(0,0),A(0,1)是正方形![]() 的两个顶点,以
的两个顶点,以![]() 对角线为边作正方形
对角线为边作正方形![]() ,再以正方形的对角线
,再以正方形的对角线![]() 作正方形
作正方形![]() ,…,依此规律,则点
,…,依此规律,则点![]() 的坐标是( )
的坐标是( )

A. (-8,0) B. (0,8)
C. (0,8![]() ) D. (0,16)
) D. (0,16)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在平行四边形ABCD中,AC、BD相交于O点,点E、F分别为BO、DO的中点,连接AF,CE.
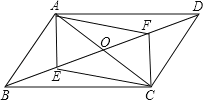
(1)求证:四边形AECF是平行四边形;
(2)如果E,F点分别在DB和BD的延长线上时,且满足BE=DF,上述结论仍然成立吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点A,B,O,C为数轴上四点,点A对应数a(a<﹣2),点O对应0,点C对应3,AB=2 (AB表示点A到点B的距离).
(1)填空:点C到原点O的距离 ,:点B对应的数 .(用含有a的式子)
(2)如图2,将一刻度尺放在数轴上,刻度尺上“6cm”和“8.7cm”分别对应数轴上的点O和点C,若BC=5,求a的值和点A在刻度尺上对应的刻度.
(3)如图3,在(2)的条件下,点A以1单位长度/秒的逮度向右运动,同时点C向左运动,若运动3秒时,点A和点C到原点D的距离相等,求点C的运动速度.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com