
【题目】用大小相同的小三角形摆成如图所示的图案,按照这样的规律摆放,则第n个图案中共有小三角形的个数是 . 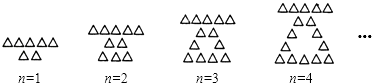
【答案】3n+4
【解析】方法一:
解:观察图形可知,第1个图形共有三角形5+2个;
第2个图形共有三角形5+3×2﹣1个;
第3个图形共有三角形5+3×3﹣1个;
第4个图形共有三角形5+3×4﹣1个;
…;
则第n个图形共有三角形5+3n﹣1=3n+4个;故答案为:3n+4
方法二:
当n=1时,s=7,当n=2时,s=10,当n=3时,s=13,
经观察,此数列为一阶等差,
∴设s=kn+b,![]() ,
,
∴ ![]() ,
,
∴s=3n+4.
观察图形可知,第1个图形共有三角形5+2个;第2个图形共有三角形5+3×2﹣1个;第3个图形共有三角形5+3×3﹣1个;第4个图形共有三角形5+3×4﹣1个;…;则第n个图形共有三角形5+3n﹣1=3n+4个;


科目:初中数学 来源: 题型:
【题目】某商场销售一种进价为20元/台的台灯,经调查发现,该台灯每天的销售量与销售单价基本满足一次函数关系,并且当销售单价为26元时,每天销售量28台;当销售单价为32元时,每天销售量16台,设台灯的销售单价为x(元),每天的销售量为y(台).
(1)求y与x之间的函数关系式;
(2)当销售单价定为多少元时,每天的利润最大?最大利润是多少?
(3)若该商场每天想获得150元的利润,在保证销售量尽可能大的前提下,应将销售单价定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ACDE是证明勾股定理时用到的一个图形,a、b、c是Rt△ABC和Rt△BED边长,易知AE=![]() c,这时我们把关于x的形如ax+
c,这时我们把关于x的形如ax+![]() cx+b=0的一元二次方程称为“勾系一元二次方程”.
cx+b=0的一元二次方程称为“勾系一元二次方程”.

请解决下列问题:
写出一个“勾系一元二次方程”;
求证:关于x的“勾系一元二次方程”ax+![]() cx+b=0必有实数根;
cx+b=0必有实数根;
若x=1是“勾系一元二次方程”ax+![]() cx+b=0的一个根,且四边形ACDE的周长是
cx+b=0的一个根,且四边形ACDE的周长是![]() ,求△ABC面积.
,求△ABC面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九(3)班为了组队参加学校举行的“五水共治”知识竞赛,在班里选取了若干名学生,分成人数相同的甲、乙两组,进行了四次“五水共治”模拟竞赛,成绩优秀的人数和优秀率分别绘制成如图统计图. 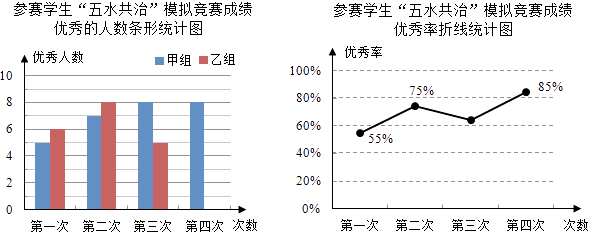
根据统计图,解答下列问题:
(1)第三次成绩的优秀率是多少?并将条形统计图补充完整;
(2)已求得甲组成绩优秀人数的平均数 ![]() =7,方差
=7,方差 ![]() =1.5,请通过计算说明,哪一组成绩优秀的人数较稳定?
=1.5,请通过计算说明,哪一组成绩优秀的人数较稳定?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O(0,0),A(0,1)是正方形![]() 的两个顶点,以
的两个顶点,以![]() 对角线为边作正方形
对角线为边作正方形![]() ,再以正方形的对角线
,再以正方形的对角线![]() 作正方形
作正方形![]() ,…,依此规律,则点
,…,依此规律,则点![]() 的坐标是( )
的坐标是( )

A. (-8,0) B. (0,8)
C. (0,8![]() ) D. (0,16)
) D. (0,16)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校实施新课程改革以来,学生的学习能力有了很大提高.王老师为进一步了解本班学生自主学习、合作交流的现状,对该班部分学生进行调查,把调查结果分为四类(A.特别好,B.好,C.一般,D.较差)后,再将调查结果绘制成两幅不完整的统计图(如图).请根据统计图解答下列问题: 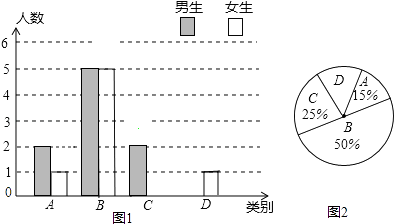
(1)本次调查中,王老师一共调查了名学生;
(2)将两幅统计图中不完整的部分补充完整;
(3)假定全校各班实施新课程改革效果一样,全校共有学生2 400人,请估计该校新课程改革效果达到A类的有多少学生;
(4)为了共同进步,王老师从被调查的A类和D类学生中分别选取一名学生进行“兵教兵”互助学习,请用列表或画树状图的方法求出恰好选中一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在平行四边形ABCD中,AC、BD相交于O点,点E、F分别为BO、DO的中点,连接AF,CE.
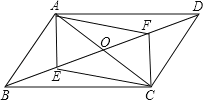
(1)求证:四边形AECF是平行四边形;
(2)如果E,F点分别在DB和BD的延长线上时,且满足BE=DF,上述结论仍然成立吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上点A对应的数为![]() ,点B对应的数为
,点B对应的数为![]() ,且多项式
,且多项式![]() 的二次项系数为
的二次项系数为![]() ,常数项为
,常数项为![]() .
.
(1)直接写出:![]() ;
;
(2)数轴上点A、B之间有一动点P,若点P对应的数为![]() ,试化简
,试化简![]() ;
;
(3)若点M从点A出发,以每秒1个单位长度的速度沿数轴向右移动;同时点N从点B出发,沿数轴每秒2个单位长度的速度向左移动,到达A点后立即返回并向右继续移动,求经过多少秒后,M、N两点相距1个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
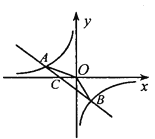
【题目】如图,已知A(-4,n),B(2,-4)是一次函数![]() 的图像和反比例函数
的图像和反比例函数![]() 的图像的两个交点.
的图像的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求不等式![]() 的解集_________(请直接写出答案).
的解集_________(请直接写出答案).
(3)求△AOB的面积;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com