
【题目】数轴上点A对应的数为![]() ,点B对应的数为
,点B对应的数为![]() ,且多项式
,且多项式![]() 的二次项系数为
的二次项系数为![]() ,常数项为
,常数项为![]() .
.
(1)直接写出:![]() ;
;
(2)数轴上点A、B之间有一动点P,若点P对应的数为![]() ,试化简
,试化简![]() ;
;
(3)若点M从点A出发,以每秒1个单位长度的速度沿数轴向右移动;同时点N从点B出发,沿数轴每秒2个单位长度的速度向左移动,到达A点后立即返回并向右继续移动,求经过多少秒后,M、N两点相距1个单位长度?
【答案】(1)2,5;(2)x+8;(3)经过2秒或![]() 秒或7秒或8秒后,M、N两点相距1个单位长度.
秒或7秒或8秒后,M、N两点相距1个单位长度.
【解析】
(1)根据多项式的系数即可得出结论;
(2)先确定出x的范围,进而得出2x+4>0,x5<0,6x>0,最后去掉绝对值,合并即可得出结论;
(3)分点N未到达点A之前和之后,建立方程求解即可得出结论.
(1)∵多项式6x3y2xy+5的二次项系数为a,常数项为b,
∴a=2,b=5,
故答案为:2,5;
(2)∴数轴上点A对应的数为a,点B对应的数为b,
∴数轴上点A对应的数为2,点B对应的数为5,
∵数轴上点A、B之间有一动点P,点P对应的数为x,
∴2<x<5,
∴2x+4>0,x5<0,6x>0,
∴|2x+4|+2|x5||6x|=2x+42(x5)(6x)=2x+42x+106+x=x+8;
(3)设经过t秒后,M、N两点相距1个单位长度,
由运动知,AM=t,BN=2t,
①当点N到达点A之前时,
a、当M,N相遇前,M、N两点相距1个单位长度,
∴t+1+2t=5+2,
∴t=2秒,
b、当M,N相遇后,M、N两点相距1个单位长度,
∴t+2t1=5+2,
∴t=![]() 秒,
秒,
②当点N到达点A之后时,
a、当N未追上M时,M、N两点相距1个单位长度,
∴t[2t(5+2)]=1,
∴t=7秒;
b、当N追上M后时,M、N两点相距1个单位长度,
∴[2t(5+2)]t=1,
∴t=8秒;
即:经过2秒或![]() 秒或7秒或8秒后,M、N两点相距1个单位长度.
秒或7秒或8秒后,M、N两点相距1个单位长度.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AC=4,BD=6,P是BD上的任一点,过点P作EF∥AC,与平行四边形的两条边分别交于点E、F,设BP=x,EF=y,则能反映y与x之间关系的图象是( ) 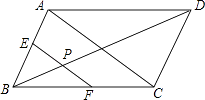
A.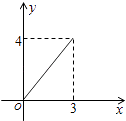
B.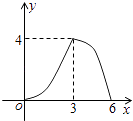
C.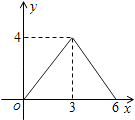
D.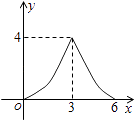
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小明,小红等同学随父母一同去某景点旅游,在购买门票时,小明和小红有图1所示的对话,根据图2的门票票价和图1所示的对话内容完成下列问题.
(1)他们一共去了几个成人几个学生?
(2)请你帮他们算一算,用哪种方式买票更省钱,省多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在300米环形跑道上练习长跑,甲的速度是6米/秒,乙的速度是7米/秒.
(1)如果甲、乙两人同地背向跑,乙先跑2秒,再经过多少秒两人相遇?
(2)如果甲、乙两人同地同向跑,乙跑几圈后能首次追上甲?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学团委会为了解该校学生的课余活动情况,采取抽样的办法,从阅读、运动、娱乐、其它等四个方面调查了若干名学生的兴趣爱好,并将调查结果绘制了如下的两幅不完整的统计图(如图),请你根据图中提供的信息解答下列问题:
(1)这次抽样中,一共调查了多少名学生?
(2)“其它”在扇形图中所占的圆心角是多少度?
(3)若该校有2500名学生,你估计全校可能有多少名学生爱好阅读?
查看答案和解析>>
科目:初中数学 来源: 题型:
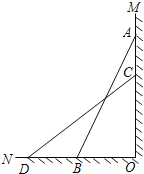
【题目】某研究性学习小组进行了探究活动.如图,已知一架竹梯AB斜靠在墙角MON处,竹梯AB=13m,梯子底端离墙角的距离BO=5m.
(1)求这个梯子顶端A距地面有多高;
(2)如果梯子的顶端A下滑4 m到点C,那么梯子的底部B在水平方向上滑动的距离BD=4 m吗?为什么?
(3)亮亮在活动中发现无论梯子怎么滑动,在滑动的过程中梯子上总有一个定点到墙角O的距离始终是不变的定值,会思考问题的你能说出这个点并说明其中的道理吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上点A、点B对应的数分别为![]() 、6.
、6.
![]() 、B两点的距离是______;
、B两点的距离是______;
![]() 当
当![]() 时,求出数轴上点C表示的有理数;
时,求出数轴上点C表示的有理数;
![]() 一元一次方解应用题:点D以每秒4个单位长度的速度从点B出发沿数轴向左运动,点E以每秒3个单位长度的速度从点A出发沿数轴向右运动,点F从原点出发沿数轴运动,点D、点E、点F同时出发,t秒后点D、点E相距1个单位长度,此时点D、点F重合,求出点F的速度及方向.
一元一次方解应用题:点D以每秒4个单位长度的速度从点B出发沿数轴向左运动,点E以每秒3个单位长度的速度从点A出发沿数轴向右运动,点F从原点出发沿数轴运动,点D、点E、点F同时出发,t秒后点D、点E相距1个单位长度,此时点D、点F重合,求出点F的速度及方向.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com