
【题目】已知数轴上点A、点B对应的数分别为![]() 、6.
、6.
![]() 、B两点的距离是______;
、B两点的距离是______;
![]() 当
当![]() 时,求出数轴上点C表示的有理数;
时,求出数轴上点C表示的有理数;
![]() 一元一次方解应用题:点D以每秒4个单位长度的速度从点B出发沿数轴向左运动,点E以每秒3个单位长度的速度从点A出发沿数轴向右运动,点F从原点出发沿数轴运动,点D、点E、点F同时出发,t秒后点D、点E相距1个单位长度,此时点D、点F重合,求出点F的速度及方向.
一元一次方解应用题:点D以每秒4个单位长度的速度从点B出发沿数轴向左运动,点E以每秒3个单位长度的速度从点A出发沿数轴向右运动,点F从原点出发沿数轴运动,点D、点E、点F同时出发,t秒后点D、点E相距1个单位长度,此时点D、点F重合,求出点F的速度及方向.
![]()
【答案】(1) A、B两点的距离是 10;(2) 数轴上点C表示的有理数是1或11;(3) 点F的速度是![]() 个单位长度/秒
个单位长度/秒
【解析】
(1)根据两点间的距离公式计算即可求解;
(2)设C表示的有理数为x,分两种情况进行列方程即可求C表示的有理数;
(3)先根据D、E、F路程差关系,求出相遇的时间,再设F的速度为y,再根据路程差关系可列方程求解.
(1)6﹣(﹣4)=10,
故A、B两点的距离是 10;
(2)设C表示的有理数为x,
两种情况分别是x<6或x>6,
6﹣x=10÷2或x﹣6=10÷2,
解得:x=1或x=11,,
故数轴上点C表示的有理数是1或11;
(3)10t=8t+10,
t=5(秒)
5y+6=10×5,
解得:y=![]() (个单位长度/秒).
(个单位长度/秒).
答:点F的速度是![]() 个单位长度/秒.
个单位长度/秒.


科目:初中数学 来源: 题型:
【题目】数轴上点A对应的数为![]() ,点B对应的数为
,点B对应的数为![]() ,且多项式
,且多项式![]() 的二次项系数为
的二次项系数为![]() ,常数项为
,常数项为![]() .
.
(1)直接写出:![]() ;
;
(2)数轴上点A、B之间有一动点P,若点P对应的数为![]() ,试化简
,试化简![]() ;
;
(3)若点M从点A出发,以每秒1个单位长度的速度沿数轴向右移动;同时点N从点B出发,沿数轴每秒2个单位长度的速度向左移动,到达A点后立即返回并向右继续移动,求经过多少秒后,M、N两点相距1个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
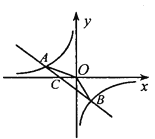
【题目】如图,已知A(-4,n),B(2,-4)是一次函数![]() 的图像和反比例函数
的图像和反比例函数![]() 的图像的两个交点.
的图像的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求不等式![]() 的解集_________(请直接写出答案).
的解集_________(请直接写出答案).
(3)求△AOB的面积;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据如下解方程![]() =
=![]() 的过程,仿照实例在每个步骤前面的括号内填写该步骤的名称,后面的括号内填写这样变形的依据,在最后的横线上写出方程的解.
的过程,仿照实例在每个步骤前面的括号内填写该步骤的名称,后面的括号内填写这样变形的依据,在最后的横线上写出方程的解.
解:原方程可变形为![]() .(分数的基本性质)
.(分数的基本性质)
去分母,得3(3x+5)=2(x–1).(__________)
去括号,得9x+15=2x–2.(__________)
(__________),得9x–2x=–15–2.(__________)
合并同类项,得7x=–17.
(__________),得x=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列变形中:
①由方程![]() =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;
②由方程![]() x=
x=![]() 两边同除以
两边同除以![]() ,得x=1;
,得x=1;
③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣![]() 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).
错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D为AB的中点,DE∥BC,交AC于点E,DE∥AC,交BC于点F.
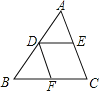
(1)求证:DE=BF;
(2)连接EF,请你猜想线段EF和AB有何关系?并对你的猜想加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2015年的政府工作报告中提出了九大热词,某数学兴趣小组就A互联网+、B民生底线、C中国制造2.0、D能耗强度等四个热词进行了抽样调查,每个同学只能从中选择一个“我最关注”的热词,如图是根据调查结果绘制的两幅不完整的统计图. 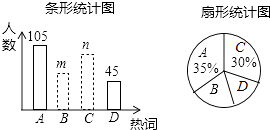
请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了名同学;
(2)条形统计图中,m= , n=;
(3)扇形统计图中,热词B所在扇形的圆心角的度数是;
(4)从该校学生中随机抽取一个最关注热词D的学生的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC的顶点B在反比例函数y= ![]() 的图象上,AC边在x轴上,已知∠ACB=90°,∠A=30°,BC=4,则图中阴影部分的面积是 .
的图象上,AC边在x轴上,已知∠ACB=90°,∠A=30°,BC=4,则图中阴影部分的面积是 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com