
【题目】用小立方块搭一几何体,使得它的从正面看和从上面看形状图如图所示,这样的几何体最少要______个立方块,最多要_______个立方块.

科目:初中数学 来源: 题型:
【题目】甲、乙两人在300米环形跑道上练习长跑,甲的速度是6米/秒,乙的速度是7米/秒.
(1)如果甲、乙两人同地背向跑,乙先跑2秒,再经过多少秒两人相遇?
(2)如果甲、乙两人同地同向跑,乙跑几圈后能首次追上甲?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+1过A(1,0)、B,(5,0)两点.
(1)求:抛物线的函数表达式;
(2)求:抛物线与y轴的交点C的坐标及其对称轴
(3)若抛物线对称轴上有一点P,使△COA∽△APB,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两会期间,记者随机抽取参会的部分代表,对他们某天发言的次数进行了统计,其结果如表,并绘制了如图所示的两幅不完整的统计图,请结合图中相关数据回答下列问题:
发言次数n | |
A | 0≤n<3 |
B | 3≤n<6 |
C | 6≤n<9 |
D | 9≤n<12 |
E | 12≤n<15 |
F | 15≤n<18 |
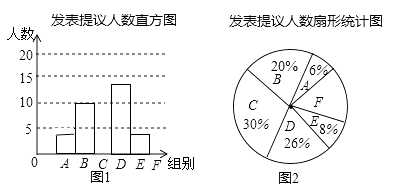
(1)求得样本容量为 , 并补全直方图;
(2)如果会议期间组织1700名代表参会,请估计在这一天里发言次数不少于12次的人数;
(3)已知A组发表提议的代表中恰有1为女士,E组发表提议的代表中只有2位男士,现从A组与E组中分别抽一位代表写报告,请用列表法或画树状图的方法,求所抽的两位代表恰好都是男士的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上点A、点B对应的数分别为![]() 、6.
、6.
![]() 、B两点的距离是______;
、B两点的距离是______;
![]() 当
当![]() 时,求出数轴上点C表示的有理数;
时,求出数轴上点C表示的有理数;
![]() 一元一次方解应用题:点D以每秒4个单位长度的速度从点B出发沿数轴向左运动,点E以每秒3个单位长度的速度从点A出发沿数轴向右运动,点F从原点出发沿数轴运动,点D、点E、点F同时出发,t秒后点D、点E相距1个单位长度,此时点D、点F重合,求出点F的速度及方向.
一元一次方解应用题:点D以每秒4个单位长度的速度从点B出发沿数轴向左运动,点E以每秒3个单位长度的速度从点A出发沿数轴向右运动,点F从原点出发沿数轴运动,点D、点E、点F同时出发,t秒后点D、点E相距1个单位长度,此时点D、点F重合,求出点F的速度及方向.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx过A(4,0),B(1,3)两点,点C,B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.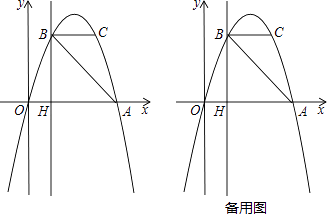
(1)求抛物线的表达式;
(2)直接写出点C的坐标,并求出△ABC的面积;
(3)点P是抛物线上一动点,且位于第四象限,当△ABP的面积为6时,求出点P的坐标;
(4)若点M在直线BH上运动,点N在x轴上运动,当CM=MN,且∠CMN=90°时,求此时△CMN的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明去文具用品商店给同学买某品牌水性笔,已知甲、乙两商店都有该品牌的水性笔且标价都是1.50元/支,但甲、乙两商店的优惠条件有所不同.甲商店:若购买不超过10支,则按标价付款;若一次性购10支以上,则超过10支的部分按标价的60%付款.乙商店:按标价的80%付款.在水性笔的质量等各种因素相同的条件下.
(1)设小明要购买的该品牌水笔数是![]() (
(![]() >10)支,请用含
>10)支,请用含![]() 的代数式分别表示在甲、乙两个商店购买该品牌水性笔的费用.
的代数式分别表示在甲、乙两个商店购买该品牌水性笔的费用.
(2)若小明要购买该品牌笔30支,你认为在甲、乙两商店中,到哪个商店购买比较省钱?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
阅读材料:
数轴是学习有理数的一种重要工具,任何有理数都可以用数轴上的点表示,这样能够运用数形结合的方法解决一些问题.例如,两个有理数在数轴上对应的点之间的距离可以用这两个数的差的绝对值表示;
在数轴上,有理数3与1对应的两点之间的距离为|3﹣1|=2;
在数轴上,有理数5与﹣2对应的两点之间的距离为|5﹣(﹣2)|=7;
在数轴上,有理数﹣2与3对应的两点之间的距离为|﹣2﹣3|=5;
在数轴上,有理数﹣8与﹣5对应的两点之间的距离为|﹣8﹣(﹣5)|=3;……
如图1,在数轴上有理数a对应的点为点A,有理数b对应的点为点B,A,B两点之间的距离表示为|a﹣b|或|b﹣a|,记为|AB|=|a﹣b|=|b﹣a|.

解决问题:
(1)数轴上有理数﹣10与﹣5对应的两点之间的距离等于 ;数轴上有理数x与﹣5对应的两点之间的距离用含x的式子表示为 ;若数轴上有理数x与﹣1对应的两点A,B之间的距离|AB|=2,则x等于 ;
联系拓广:
(2)如图2,点M,N,P是数轴上的三点,点M表示的数为4,点N表示的数为﹣2,动点P表示的数为x.
请从A,B两题中任选一题作答,我选择 题.
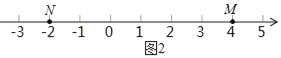
A.①若点P在点M,N两点之间,则|PM|+|PN|= ;
②若|PM|=2|PN|,即点P到点M的距离等于点P到点N的距离的2倍,则x等于 .
B.①若点P在点M,N之间,则|x+2|+|x﹣4|= ;
若|x+2|+|x﹣4|═10,则x= ;
②根据阅读材料及上述各题的解答方法,|x+2|+|x|+|x﹣2|+|x﹣4|的最小值等于 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com