
【题目】解方程
(1)3x﹣7+4x=6x﹣2
(2)4﹣3(2﹣x)=5x
(3)2(x+3)﹣5(1﹣x)=3(x﹣1)
(4)![]() .
.
【答案】(1)x=5.(2)x=﹣1.(3)x=﹣1.(4)x=﹣9.
【解析】
(1)根据一元一次方程的解法一步步解方程,即可得出方程的解;
(2)根据一元一次方程的解法一步步解方程,即可得出方程的解;
(3)根据一元一次方程的解法一步步解方程,即可得出方程的解;
(4)根据一元一次方程的解法一步步解方程,即可得出方程的解.
(1)移项,得:3x+4x﹣6x=﹣2+7,
合并同类项,得:x=5.
(2)去括号,得:4﹣6+3x=5x,
移项,得:3x﹣5x=﹣4+6,
合并同类项,得:﹣2x=2,
系数化为1,得:x=﹣1.
(3)去括号,得:2x+6﹣5+5x=3x﹣3,
移项,得:2x+5x﹣3x=﹣3﹣6+5,
合并同类项,得:4x=﹣4,
系数化为1,得:x=﹣1.
(4)去分母,得:5(x﹣3)﹣2(4x+1)=10,
去括号,得:5x﹣15﹣8x﹣2=10,
移项,得:5x﹣8x=10+15+2,
合并同类项,得:﹣3x=27,
系数化为1,得:x=﹣9.


科目:初中数学 来源: 题型:
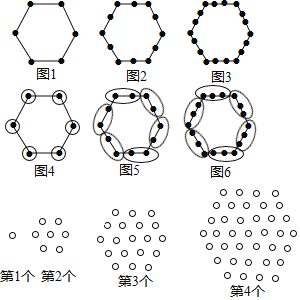
【题目】“分块计数法”:对有规律的图形进行计数时,有些题可以采用“分块计数”的方法.
例如:图1有6个点,图2有12个点,图3有18个点,……,按此规律,求图10、图n有多少个点?
我们将每个图形分成完全相同的6块,每块黑点的个数相同(如图),这样图1中黑点个数是6×1=6个;图2中黑点个数是6×2=12个:图3中黑点个数是6×3=18个;所以容易求出图10、图n中黑点的个数分别是 、 .
请你参考以上“分块计数法”,先将下面的点阵进行分块(画在答题卡上),再完成以下问题:
(1)第5个点阵中有 个圆圈;第n个点阵中有 个圆圈.
(2)小圆圈的个数会等于271吗?如果会,请求出是第几个点阵.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种进价为20元/台的台灯,经调查发现,该台灯每天的销售量与销售单价基本满足一次函数关系,并且当销售单价为26元时,每天销售量28台;当销售单价为32元时,每天销售量16台,设台灯的销售单价为x(元),每天的销售量为y(台).
(1)求y与x之间的函数关系式;
(2)当销售单价定为多少元时,每天的利润最大?最大利润是多少?
(3)若该商场每天想获得150元的利润,在保证销售量尽可能大的前提下,应将销售单价定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,AC与BD相交于点O,连接CD
(1)求∠AOD的度数;
(2)求证:四边形ABCD是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司装修需用A型板材240块,B型板材180块,A型板材规格是60cm×30cm,B型板材规格是40cm×30cm.现只能购得规格是150cm×30cm的标准板材.一张标准板材尽可能多地裁出A型、B型板材,共有下列三种裁法:(如图是裁法一的裁剪示意图) 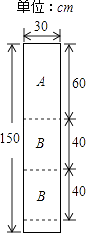
裁法一 | 裁法二 | 裁法三 | |
A型板材块数 | 1 | 2 | 0 |
B型板材块数 | 2 | m | n |
(1)上表中,m= , n=;
(2)若裁完剩余的部分可以拼接成A型或B型板材使用,则至少需要几张标准板材?
(3)若裁完剩余的部分不能拼接成A型或B型板材使用,已知用170张标准板材,可以完成装修任务.请通过计算写出两种剪裁方案(要求:①其中一种方案三种剪裁方法都使用,另一种方案只用到两种剪裁方法;②每种方案需写出使用各种裁剪方法裁剪标准板的张数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ACDE是证明勾股定理时用到的一个图形,a、b、c是Rt△ABC和Rt△BED边长,易知AE=![]() c,这时我们把关于x的形如ax+
c,这时我们把关于x的形如ax+![]() cx+b=0的一元二次方程称为“勾系一元二次方程”.
cx+b=0的一元二次方程称为“勾系一元二次方程”.

请解决下列问题:
写出一个“勾系一元二次方程”;
求证:关于x的“勾系一元二次方程”ax+![]() cx+b=0必有实数根;
cx+b=0必有实数根;
若x=1是“勾系一元二次方程”ax+![]() cx+b=0的一个根,且四边形ACDE的周长是
cx+b=0的一个根,且四边形ACDE的周长是![]() ,求△ABC面积.
,求△ABC面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九(3)班为了组队参加学校举行的“五水共治”知识竞赛,在班里选取了若干名学生,分成人数相同的甲、乙两组,进行了四次“五水共治”模拟竞赛,成绩优秀的人数和优秀率分别绘制成如图统计图. 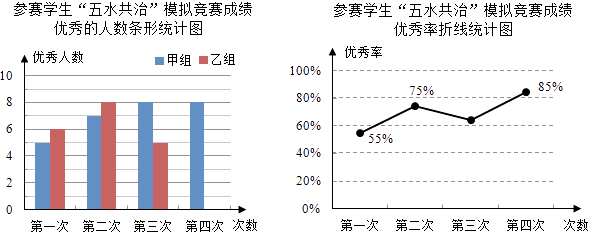
根据统计图,解答下列问题:
(1)第三次成绩的优秀率是多少?并将条形统计图补充完整;
(2)已求得甲组成绩优秀人数的平均数 ![]() =7,方差
=7,方差 ![]() =1.5,请通过计算说明,哪一组成绩优秀的人数较稳定?
=1.5,请通过计算说明,哪一组成绩优秀的人数较稳定?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上点A对应的数为![]() ,点B对应的数为
,点B对应的数为![]() ,且多项式
,且多项式![]() 的二次项系数为
的二次项系数为![]() ,常数项为
,常数项为![]() .
.
(1)直接写出:![]() ;
;
(2)数轴上点A、B之间有一动点P,若点P对应的数为![]() ,试化简
,试化简![]() ;
;
(3)若点M从点A出发,以每秒1个单位长度的速度沿数轴向右移动;同时点N从点B出发,沿数轴每秒2个单位长度的速度向左移动,到达A点后立即返回并向右继续移动,求经过多少秒后,M、N两点相距1个单位长度?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com