
【题目】如图1(注:与图2完全相同),二次函数y=![]() x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.
x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.
(1)求该二次函数的解析式;
(2)设该抛物线的顶点为D,求△ACD的面积;
(3)若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动,当P,Q运动到t秒时,△APQ沿PQ所在的直线翻折,点A恰好落在抛物线上E点处,请直接判定此时四边形APEQ的形状,并求出E点坐标.

【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣4;(2)4;(3)四边形APEQ为菱形,E点坐标为(﹣
x﹣4;(2)4;(3)四边形APEQ为菱形,E点坐标为(﹣![]() ,﹣
,﹣![]() ).理由详见解析.
).理由详见解析.
【解析】试题分析:(1)将A,B点坐标代入函数y=![]() x2+bx+c中,求得b、c,进而可求解析式;(2)由解析式先求得点D、C坐标,再根据S△ACD=S梯形AOMD﹣S△CDM﹣S△AOC,列式计算即可;(3)注意到P,Q运动速度相同,则△APQ运动时都为等腰三角形,又由A、E对称,则AP=EP,AQ=EQ,易得四边形四边都相等,即菱形.利用菱形对边平行且相等的性质可用t表示E点坐标,又E在E函数上,所以代入即可求t,进而E可表示.
x2+bx+c中,求得b、c,进而可求解析式;(2)由解析式先求得点D、C坐标,再根据S△ACD=S梯形AOMD﹣S△CDM﹣S△AOC,列式计算即可;(3)注意到P,Q运动速度相同,则△APQ运动时都为等腰三角形,又由A、E对称,则AP=EP,AQ=EQ,易得四边形四边都相等,即菱形.利用菱形对边平行且相等的性质可用t表示E点坐标,又E在E函数上,所以代入即可求t,进而E可表示.
试题解析:(1)∵二次函数y=![]() x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0),
x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0),
∴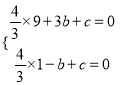 ,
,
解得: 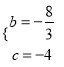 ,
,
∴y=![]() x2﹣
x2﹣![]() x﹣4;
x﹣4;
(2)过点D作DM⊥y轴于点M,
∵y=![]() x2﹣
x2﹣![]() x﹣4=
x﹣4=![]() (x﹣1)2﹣
(x﹣1)2﹣![]() ,
,
∴点D(1,﹣![]() )、点C(0,﹣4),
)、点C(0,﹣4),
则S△ACD=S梯形AOMD﹣S△CDM﹣S△AOC=![]() ×(1+3)×
×(1+3)×![]() ﹣
﹣![]() ×(
×(![]() ﹣4)×1﹣
﹣4)×1﹣![]() ×3×4=4;
×3×4=4;
(3)四边形APEQ为菱形,E点坐标为(﹣![]() ,﹣
,﹣![]() ).理由如下
).理由如下
如图2,E点关于PQ与A点对称,过点Q作,QF⊥AP于F,
∵AP=AQ=t,AP=EP,AQ=EQ
∴AP=AQ=QE=EP,
∴四边形AQEP为菱形,
∵FQ∥OC,
∴![]() ,
,
∴![]()
∴AF=![]() t,FQ=
t,FQ=![]() t
t
∴Q(3﹣![]() t,﹣
t,﹣![]() t),
t),
∵EQ=AP=t,
∴E(3﹣![]() t﹣t,﹣
t﹣t,﹣![]() t),
t),
∵E在二次函数y=![]() x2﹣
x2﹣![]() x﹣4上,
x﹣4上,
∴﹣![]() t=
t=![]() (3﹣
(3﹣![]() t)2﹣
t)2﹣![]() (3﹣
(3﹣![]() t)﹣4,
t)﹣4,
∴t=![]() ,或t=0(与A重合,舍去),
,或t=0(与A重合,舍去),
∴E(﹣![]() ,﹣
,﹣![]() ).
).



 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】锐锐参加我市电视台组织的“牡丹杯”智力竞答节目,答对最后两道单选题就顺利通关,第一道单选题有3个选项,第二道单选题有4个选项,这两道题锐锐都不会,不过锐锐还有两个“求助”可以用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项).
(1)如果锐锐两次“求助”都在第一道题中使用,那么锐锐通关的概率是________;
(2)如果锐锐两次“求助”都在第二道题中使用,那么锐锐通关的概率是________;
(3)如果锐锐每道题各用一次“求助”,请用树状图或者列表来分析他顺利通关的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小型企业实行工资与业绩挂钩制度,工人工资分为A、B、C、D四个档次.小明对该企业三月份工人工资进行调查,并根据收集到的数据,绘制了如下尚不完整的统计表与扇形统计图.
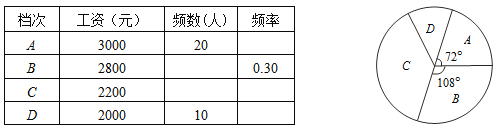
根据上面提供的信息,回答下列问题:
(1)求该企业共有多少人?
(2)请将统计表补充完整;
(3)扇形统计图中“C档次”的扇形所对的圆心角是 度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为更好地开展“传统文化进校园”活动,随机抽查了部分学生,了解他们最喜爱的传统文化项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布直方图.
最喜爱的传统文化项目类型频数分布表


根据以上信息完成下列问题:
(1)直接写出频数分布表中a的值;
(2)补全频数分布直方图;
(3)若全校共有学生1500名,估计该校最喜爱围棋的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠AOB内一点P,P1,P2分别P是关于OA、OB的对称点,P1P2交OA于M,交OB于N,若P1P2=6cm,则△PMN的周长是( )
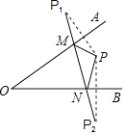
A.3cmB.4cmC.5cmD.6cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着退耕还林政策的进一步落实,三岗村从2015年底到2017年底林地面积变化如图所示,则2016,2017这两年三岗村林地面积年平均增长的百分率为( )
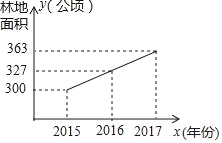
A. 7% B. 10% C. 11% D. 21%
查看答案和解析>>
科目:初中数学 来源: 题型:
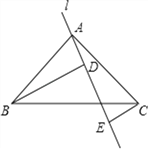
【题目】如图,Rt△ABC中,AB=AC,∠BAC=90°,直线l为经过点A的任一直线,BD⊥l于D,CE⊥AE,若BD>CE,试问:
(1)AD与CE的大小关系如何?请说明理由;
(2)线段BD,DE,CE之间的数量之间关系如何?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
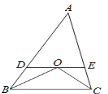
【题目】如图,在△ABC中,∠B与∠C的平分线交于点O,过点O作DE∥BC,分别交AB,AC于点D,E.若AB=5,AC=4,则△ADE的周长是______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠CFE为________度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com