
【题目】如图,在△ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠CFE为________度.

【答案】50°
【解析】
连接OB,OC,先求出∠BAO=25°,进而求出∠OBC=40°,求出∠COE=∠OCB=40°,最后根据等腰三角形的性质,问题即可解决.
解:如图,连接OB,
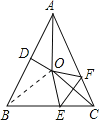
∵∠BAC=50°,AO为∠BAC的平分线,
∴∠BAO=![]() ∠BAC=
∠BAC=![]() ×50°=25°.
×50°=25°.
又∵AB=AC,
∴∠ABC=∠ACB=65°.
∵DO是AB的垂直平分线,
∴OA=OB,
∴∠ABO=∠BAO=25°,
∴∠OBC=∠ABC-∠ABO=65°-25°=40°.
∵AO为∠BAC的平分线,AB=AC,
∴直线AO垂直平分BC,
∴OB=OC,
∴∠OCB=∠OBC=40°,
∵将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,
∴OE=CE.
∴∠COE=∠OCB=40°;
在△OCE中,∠OEC=180°-∠COE-∠OCB=180°-40°-40°=100°,
∴∠CEF=![]() ∠CEO=50°.
∠CEO=50°.
故答案为:50°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某科技有限公司准备购进A和B两种机器人来搬运化工材料,已知购进A种机器人2个和B种机器人3个共需16万元;购进A种机器人3个和B种机器人2个共需14万元.请解答下列问题:
(1)求A , B两种机器人每个的进价;
(2)已知该公司购买B种机器人的个数比购买A种机器人的个数的2倍多4个,如果需要购买A、B两种种机器人的总个数不少于28个,且该公司购买的A、B两种种机器人的总费用不超过106万元,那么该公司有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,BC∥OA,∠B=∠A=100°,试回答下列问题:

(1)如图①,求证:OB∥AC.
(2)如图②,若点E、F在线段BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF.求∠EOC的度数.
(3)在(2)的条件下,若平行移动AC,如图③,那么∠OCB:∠OFB的值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,AD是△ABC的内角平线,交BC于D点,DE⊥AB,DF⊥AC,垂足分别为E、F,连结EF,
(1)请根据上述几何语言,画出完整的图形,作∠BAC的角平分线AD要求尺规作图,(保留作图痕迹,不写作法);
(2)判断AD是否为EF的垂直平分线,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分,已知抛物线的对称轴为x=2,与x轴的一个交点是(﹣1,0).下列结论:
①ac<0;
②4a﹣2b+c>0;
③抛物线与x轴的另一个交点是(4,0);
④点(﹣3,y1),(6,y2)都在抛物线上,则有y1<y2 . 其中正确的个数为( )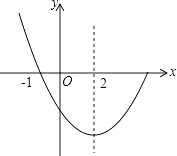
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 ![]() ABC中,AD平分
ABC中,AD平分 ![]() BAC,按如下步骤作图:
BAC,按如下步骤作图:
第一步,分别以点A、D为圆心,以大于 ![]() AD的长为半径在AD两侧做弧,交于两点M、N;
AD的长为半径在AD两侧做弧,交于两点M、N;
第二步,连接MN分别交AB、AC于点E、F;
第三步,连接DE、DF.
若BD=6,AF=4,CD=3,则BE的长是( ).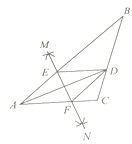
A.2
B.4
C.6
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
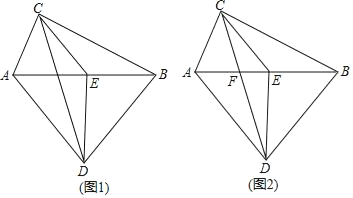
【题目】如图,已知AC⊥BC,AD⊥BD,E为AB的中点,
(1)如图1,求证:△ECD是等腰三角形;
(2)如图2,CD与AB交点为F,若AD=BD,EF=3,DE=4,求CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com