
【题目】如图,已知,BC∥OA,∠B=∠A=100°,试回答下列问题:

(1)如图①,求证:OB∥AC.
(2)如图②,若点E、F在线段BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF.求∠EOC的度数.
(3)在(2)的条件下,若平行移动AC,如图③,那么∠OCB:∠OFB的值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值.
【答案】(1)证明见解析;
(2)∠EOC的度数是40°;
(3)不改变,∠OCB:∠OFB的值为1:2.
【解析】分析:(1),首先根据平行线的性质可得∠B+∠O=180°,再根据∠A=∠B可得∠A+∠O=180°,进而得到OB∥AC;
(2)由(1)即可求出∠BOA的度数,根据角平分线的性质可得∠EOF=![]() ∠BOF,∠FOC=
∠BOF,∠FOC=![]() ∠FOA,进而得到∠EOC的大小;
∠FOA,进而得到∠EOC的大小;
(3)由BC∥OA可得∠FCO=∠COA,进而得到∠FOC=∠FCO,故∠OFB=∠FOC+∠FCO=2∠OCB,进而得到∠OCB:∠OFB的值.
本题解析;(1)证明:∵BC∥OA,
∴∠B+∠O=180°,∴∠O=180°﹣∠B=80°,
而∠A=100°,∴∠A+∠O=180°,
∴OB∥AC;
(2)解:∵OE平分∠BOF,
∴∠BOE=∠FOE, 而∠FOC=∠AOC,
∴∠EOF+∠COF=![]() ∠AOB=
∠AOB=![]() ×80°=40°;
×80°=40°;
(3)解:不改变
∵BC∥OA,
∴∠OCB=∠AOC,∠OFB=∠AOF,
∵∠FOC=∠AOC,
∴∠AOF=2∠AOC,
∴∠OFB=2∠OCB,即∠OCB:∠OFB的值为1:2;


科目:初中数学 来源: 题型:
【题目】已知:AB为⊙O的直径,C是⊙O上一点,如图,AB=12,BC=4 ![]() .BH与⊙O相切于点B,过点C作BH的平行线交AB于点E.
.BH与⊙O相切于点B,过点C作BH的平行线交AB于点E.
(1)求CE的长;
(2)延长CE到F,使EF= ![]() ,连接BF并延长BF交⊙O于点G,求BG的长;
,连接BF并延长BF交⊙O于点G,求BG的长;
(3)在(2)的条件下,连接GC并延长GC交BH于点D,求证:BD=BG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平行四边形ABCD中,AC为对角线,E是边AD上一点,BE⊥AC交AC于点F,BE、CD的延长线交于点G,且∠ABE=∠CAD. 
(1)求证:四边形ABCD是矩形;
(2)如果AE=EG,求证:AC2=BCBG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB、CD为 ![]() O的直径,弦AE//CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使
O的直径,弦AE//CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使 ![]() PED=
PED= ![]() C.
C.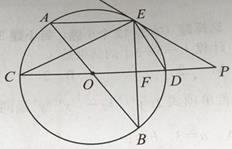
(1)求证:PE是 ![]() O的切线;
O的切线;
(2)求证:ED平分 ![]() BEP;
BEP;
(3)若 ![]() O的半径为5,CF=2EF,求PD的长.
O的半径为5,CF=2EF,求PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学初二年级抽取部分学生进行跳绳测试,并规定:每分钟跳90次以下的为不及格;每分钟跳90~99次的为及格;每分钟100~109次的为中等;每分钟110~119次的为良好;每分钟120次及以上的为优秀。测试结果整理绘制成如下两幅不完整的统计图。请根据图中信息,解答下列各题:
(1)参加这次跳绳测试的共有人;
(2)补全条形统计图;
(3)在扇形统计图中,“中等”部分所对的圆心角的度数是;
(4)如果该校初二年级的总人数是480人,根据此统计数据,请你估算出该校初二年级跳绳成绩为“优秀”的人数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,选段AB=4,以AB为直径作半圆O,点C为弧AB的中点,点P为直径AB上一点,联结PC,过点C作CD∥AB,且CD=PC,过点D作DE∥PC,交射线PB于点E,PD与CE相交于点Q. 
(1)若点P与点A重合,求BE的长;
(2)设PC=x, ![]() =y,当点P在线段AO上时,求y与x的函数关系式及定义域;
=y,当点P在线段AO上时,求y与x的函数关系式及定义域;
(3)当点Q在半圆O上时,求PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小东在教学楼距地面9米高的窗口C处,测得正前方旗杆顶部A点的仰角为37°,旗杆底部B点的俯角为45°,升旗时,国旗上端悬挂在距地面2.25米处,若国旗随国歌声冉冉升起,并在国歌播放45秒结束时到达旗杆顶端,则国旗应以多少米/秒的速度匀速上升?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)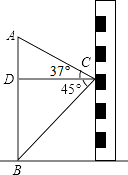
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠CFE为________度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴相交于A、B两点,点B的坐标为(3,0),与y轴相交于点C(0,﹣3),顶点为D.
(1)求出抛物线y=x2+bx+c的表达式;
(2)连结BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点,过点P作PF∥DE交抛物线于点F,设点P的横坐标为m.
①当m为何值时,四边形PEDF为平行四边形.
②设四边形OBFC的面积为S,求S的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com