Question

【题目】已知：如图，选段AB=4，以AB为直径作半圆O，点C为弧AB的中点，点P为直径AB上一点，联结PC，过点C作CD∥AB，且CD=PC，过点D作DE∥PC，交射线PB于点E，PD与CE相交于点Q．
（1）若点P与点A重合，求BE的长；
（2）设PC=x， =y，当点P在线段AO上时，求y与x的函数关系式及定义域；
（3）当点Q在半圆O上时，求PC的长．

Answer 1

【答案】
（1）解：如图1中，连接OC．

∵ = ，

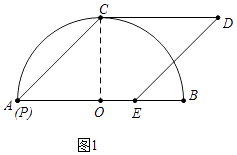
∴CO⊥AB，△AOC是等腰直角三角形，AC= OC=2 ，

∵四边形ACDE是菱形，

∴AE=AC=2 ，

∴BE=AB﹣AE=4﹣2

（2）解：如图2中，

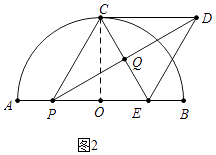
∵PC=x，OC=2，

∴OP= ，OE=x﹣ ，

∵四边形PCDE是菱形，

∴PD⊥EC，CQ=QE，PQ=QD，

∵ = =y，

∴tan∠PEQ= = ，

∴y= （2≤x≤2 ）

（3）解：如图3中，

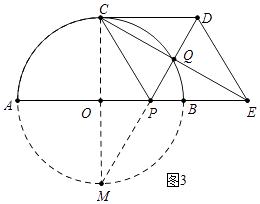
∵点Q在⊙O上，∠CQP=90°，

∴∠CQP所以对的弦CM是直径，

∵∠M+∠OPM=90°，∠QPE+∠QEP=90°，∠OPM=∠QPE，

∴∠M=∠QEP，易知∠PCM=∠M，∠PCQ=∠PEQ，

∴∠PCO=∠PCQ=∠CEO=30°，

在Rt△POC中，PC=OC÷cos30°=

【解析】（1）如图1中，连接OC．只要证明△AOC是等腰直角三角形即可．（2）由PC=x，OC=2，可得OP= ，OE=x﹣ ，由四边形PCDE是菱形，推出PD⊥EC，CQ=QE，PQ=QD，由 = =y，推出tan∠PEQ= = ，由此即可解决问题．（3）由点Q在⊙O上，∠CQP=90°，推出∠CQP所以对的弦CM是直径，由∠M+∠OPM=90°，∠QPE+∠QEP=90°，∠OPM=∠QPE，推出∠M=∠QEP，易知∠PCM=∠M，∠PCQ=∠PEQ，推出∠PCO=∠PCQ=∠CEO=30°，由此即可解决问题．