
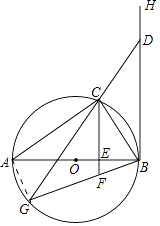
【题目】已知:AB为⊙O的直径,C是⊙O上一点,如图,AB=12,BC=4 ![]() .BH与⊙O相切于点B,过点C作BH的平行线交AB于点E.
.BH与⊙O相切于点B,过点C作BH的平行线交AB于点E.
(1)求CE的长;
(2)延长CE到F,使EF= ![]() ,连接BF并延长BF交⊙O于点G,求BG的长;
,连接BF并延长BF交⊙O于点G,求BG的长;
(3)在(2)的条件下,连接GC并延长GC交BH于点D,求证:BD=BG.
【答案】
(1)
解:∵BH与⊙O相切于点B,
∴AB⊥BH,
∵BH∥CE,
∴CE⊥AB,
∵AB是直径,
∴∠CEB=∠ACB=90°,
∵∠CBE=∠ABC,
∴△ABC∽△CBE,
∴ ![]() =
= ![]() ,
,
∵AC= ![]() =4
=4 ![]() ,
,
∴CE=4 ![]()
(2)
解:连接AG.
∵∠FEB=∠ACB=90°,∠EBF=∠ABC,
∴△ABG∽△FBE,
∴ ![]() =
= ![]() ,
,
∵BE= ![]() =4,
=4,
∴BF= ![]() =3
=3 ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴BG=8 ![]()
(3)
解:易知CF=4 ![]() +
+ ![]() =5
=5 ![]() ,
,
∴GF=BG﹣BF=5 ![]() ,
,
∴CF=GF,
∴∠FCG=∠FGC,
∵CF∥BD,
∴∠GCF=∠BDG,
∴∠BDG=∠BGD,
∴BG=BD.
【解析】(1)只要证明△ABC∽△CBE,可得 ![]() =
= ![]() ,由此即可解决问题.(2)连接AG.只要证明△ABG∽△FBE,可得
,由此即可解决问题.(2)连接AG.只要证明△ABG∽△FBE,可得 ![]() =
= ![]() ,由BE=
,由BE= ![]() =4,再求出BF,即可解决问题.(3)通过计算首先证明CF=FG,推出∠FCG=∠FGC,由CF∥BD,推出∠GCF=∠BDG,推出∠BDG=∠BGD即可证明.
=4,再求出BF,即可解决问题.(3)通过计算首先证明CF=FG,推出∠FCG=∠FGC,由CF∥BD,推出∠GCF=∠BDG,推出∠BDG=∠BGD即可证明.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对切线的性质定理的理解,了解切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.


科目:初中数学 来源: 题型:
【题目】一个不透明袋子中有1个红球,1个绿球和n个白球,这些球除颜色外无其他差别.
(1)当n=1时,从袋中随机摸出1个球,摸到红球和摸到白球的可能性是否相同?(在答题卡相应位置填“相同”或“不相同”);
(2)从袋中随机摸出一个球,记录其颜色,然后放回,大量重复该实验,发现摸到绿球的频率稳定于0.25,则n的值是
(3)在一个摸球游戏中,所有可能出现的结果如下:
根据树状图呈现的结果,求两次摸出的球颜色不同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
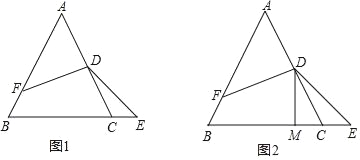
【题目】如图1,等边△ABC中,D为AC中点,∠EDF=120°,DF交AB于F点,且AF=nBF(n为常数,且n>1).
(1)求证:DF=DE;
(2)如图1,求证:AF﹣CE=![]() AB;
AB;
(3)如图2,当n= 时,过D作DM⊥BC于M点,C为EM的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
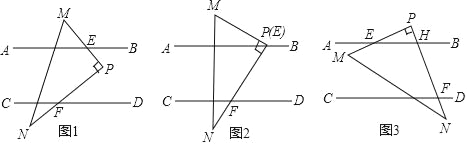
【题目】问题情境:已知:如图1,直线AB∥CD,现将直角三角板△PMN放入图中,其中∠MPN=90°,点P始终在直线MN右侧.PM交AB于点E,PN交CD于点F,试探究:∠PFD与∠AEM的数量关系.
(1)特例如图2,当点P在直线AB上(即点E与点P重合)时,直接写出∠PFD与∠AEM的数量关系,不必证明;
(2)类比探究:如图1,当点P在AB与CD之间时,猜想∠PFD与∠AEM的数量关系,并说明理由;
(3)拓展延伸:如图3,当点P在直线AB的上方时,PN交AB于点H,其他条件不变,猜想∠PFD与∠AEM的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某市市民晚饭后1小时内的生活方式,调查小组设计了“阅读”、“锻炼”、“看电视”和“其它”四个选项,用随机抽样的方法调查了该市部分市民,并根据调查结果绘制成如下统计图.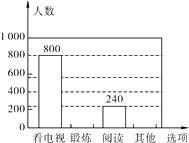
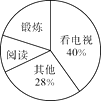
根据统计图所提供的信息,解答下列问题:
(1)本次共调查了名市民;
(2)补全条形统计图;
(3)该市共有480万市民,估计该市市民晚饭后1小时内锻炼的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某科技有限公司准备购进A和B两种机器人来搬运化工材料,已知购进A种机器人2个和B种机器人3个共需16万元;购进A种机器人3个和B种机器人2个共需14万元.请解答下列问题:
(1)求A , B两种机器人每个的进价;
(2)已知该公司购买B种机器人的个数比购买A种机器人的个数的2倍多4个,如果需要购买A、B两种种机器人的总个数不少于28个,且该公司购买的A、B两种种机器人的总费用不超过106万元,那么该公司有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,BC∥OA,∠B=∠A=100°,试回答下列问题:

(1)如图①,求证:OB∥AC.
(2)如图②,若点E、F在线段BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF.求∠EOC的度数.
(3)在(2)的条件下,若平行移动AC,如图③,那么∠OCB:∠OFB的值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com