
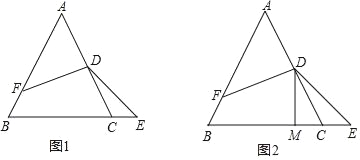
【题目】如图1,等边△ABC中,D为AC中点,∠EDF=120°,DF交AB于F点,且AF=nBF(n为常数,且n>1).
(1)求证:DF=DE;
(2)如图1,求证:AF﹣CE=![]() AB;
AB;
(3)如图2,当n= 时,过D作DM⊥BC于M点,C为EM的中点.
【答案】(1)见解析;(2)见解析;(3)3.
【解析】
(1)过D点作DG∥BC交AB于G点,证明△DGF≌△DCE,根据全等三角形的性质证明即可;
(2)根据全等三角形的性质得到GF=CE,结合图形证明;
(3)根据直角三角形的性质得到CM=![]() CD,得到GF=
CD,得到GF=![]() AG,根据等边三角形的性质解答.
AG,根据等边三角形的性质解答.
解:(1)证明:过D点作DG∥BC交AB于G点,
∵DG∥BC,
∴∠ADG=∠ACB=60°=∠A,
∴△AGD为等边三角形,
∴GD=AD=DC,
∵∠GDC=∠FDE=120°,
∴∠GDF=∠DCE,
在△DGF和△DCE中,
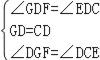
∴△DGF≌△DCE(ASA)
∴DF=DE;
(2)∵△DGF≌△DCE,
∴GF=CE,
∵DG∥BC,D为AC中点,
∴AG=![]() AB,
AB,
∴AF﹣CE=AF﹣GF=AG=![]() AB;
AB;
(3)∵DM⊥BC,∠DCM=60°,
∴CM=![]() CD,
CD,
∵C为EM的中点,
∴CE=![]() CD,
CD,
由(1)得,CE=GF,
∴GF=![]() CD,
CD,
∴GF=![]() AG=
AG=![]() GB,
GB,
∴AF=3BF,
∴n=3,
故答案为:3.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点C,D在⊙O上,点E在⊙O外,∠EAC=∠B.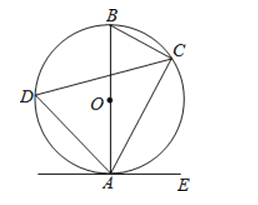
(1)求证:直线AE是⊙O的切线
(2)若∠D=60°,AB=6时,求劣弧![]() 的长(结果保留π)
的长(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在9×9的正方形网格中,△ABC三个顶点在格点上,每个小正方形的边长为1.
(1)建立适当的平面直角坐标系后,若点A的坐标为(1,1),点C的坐标为(4,2),画出平面直角坐标系并写出点B的坐标;
(2)直线l经过点A且与y轴平行,写出点B、C关于直线l对称点B1、C1的坐标;
(3)直接写出BC上一点P(a,b)关于直线l对称点P1的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2﹣4x与x轴交于O,A两点,P为抛物线上一点,过点P的直线y=x+m与对称轴交于点Q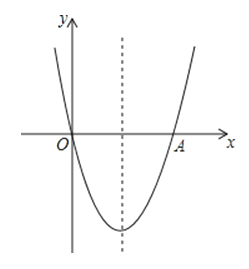
(1)这条抛物线的对称轴是 ,直线PQ与x轴所夹锐角的度数是 .
(2)若两个三角形面积满足S△POQ=![]() S△PAQ , 求m的值
S△PAQ , 求m的值
(3)当点P在x轴下方的抛物线上时,过点C(2,2)的直线AC与直线PQ交于点D,求:①PD+DQ的最大值;②PDDQ的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,东营市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如图两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题: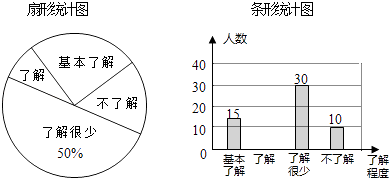
(1)接受问卷调查的学生共有 人,扇形统计图中“基本了解”部分所对应扇形的圆心角为 ;
(2)请补全条形统计图;
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数;
(4)若从对校园安全知识达到了“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AB上一点,点D为BC的中点,且AB=18cm,AC=4CD.
(1)图中共有 条线段;
(2)求AC的长;
(3)若点E在直线AB上,且EA=2cm,求BE的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:AB为⊙O的直径,C是⊙O上一点,如图,AB=12,BC=4 ![]() .BH与⊙O相切于点B,过点C作BH的平行线交AB于点E.
.BH与⊙O相切于点B,过点C作BH的平行线交AB于点E.
(1)求CE的长;
(2)延长CE到F,使EF= ![]() ,连接BF并延长BF交⊙O于点G,求BG的长;
,连接BF并延长BF交⊙O于点G,求BG的长;
(3)在(2)的条件下,连接GC并延长GC交BH于点D,求证:BD=BG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平行四边形ABCD中,AC为对角线,E是边AD上一点,BE⊥AC交AC于点F,BE、CD的延长线交于点G,且∠ABE=∠CAD. 
(1)求证:四边形ABCD是矩形;
(2)如果AE=EG,求证:AC2=BCBG.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com