
【题目】如图,C为线段AB上一点,点D为BC的中点,且AB=18cm,AC=4CD.
(1)图中共有 条线段;
(2)求AC的长;
(3)若点E在直线AB上,且EA=2cm,求BE的长.
![]()
【答案】(1)5(2)12cm(3)16cm或20cm
【解析】
(1)线段的个数为![]() ,n为点的个数.
,n为点的个数.
(2)由题意易推出CD的长度,再算出AC=4CD即可.
(3)E点可在A点的两边讨论即可.
(1)图中有四个点,线段有![]() =6.
=6.
故答案为:6;
(2)由点D为BC的中点,得
BC=2CD=2BD,
由线段的和差,得
AB=AC+BC,即4CD+2CD=18,
解得CD=3,
AC=4CD=4×3=12cm;
(3)①当点E在线段AB上时,由线段的和差,得
BE=AB﹣AE=18﹣2=16cm,
②当点E在线段BA的延长线上,由线段的和差,得
BE=AB+AE=18+2=20cm.
综上所述:BE的长为16cm或20cm.


科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD中,AD∥BC,∠BAD=90°,CE⊥AD于点E,AD=8cm,BC=4cm,AB=5cm.从初始时刻开始,动点P,Q 分别从点A,B同时出发,运动速度均为1cm/s,动点P沿A﹣B﹣﹣C﹣﹣E的方向运动,到点E停止;动点Q沿B﹣﹣C﹣﹣E﹣﹣D的方向运动,到点D停止,设运动时间为xs,△PAQ的面积为ycm2 , (这里规定:线段是面积为0的三角形)
解答下列问题:
(1)当x=2s时,y=cm2;当x= ![]() s时,y=cm2 .
s时,y=cm2 .
(2)当5≤x≤14 时,求y与x之间的函数关系式.
(3)当动点P在线段BC上运动时,求出 ![]() S梯形ABCD时x的值.
S梯形ABCD时x的值.
(4)直接写出在整个运动过程中,使PQ与四边形ABCE的对角线平行的所有x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在锐角△ABC中,D,E分别为AB,BC中点,F为AC上一点,且∠AFE=∠A,DM∥EF交AC于点M.
(1)求证:DM=DA;
(2)点G在BE上,且∠BDG=∠C,如图②,求证:△DEG∽△ECF;
(3)在图②中,取CE上一点H,使∠CFH=∠B,若BG=1,求EH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,等边△ABC中,D为AC中点,∠EDF=120°,DF交AB于F点,且AF=nBF(n为常数,且n>1).
(1)求证:DF=DE;
(2)如图1,求证:AF﹣CE=![]() AB;
AB;
(3)如图2,当n= 时,过D作DM⊥BC于M点,C为EM的中点.
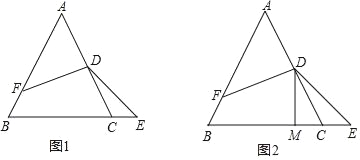
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB>AC , 分别以点B和点C为圆心,大于BC一半的长为半径作圆弧,两弧相交于点M和点N , 作直线MN交AB于点D;连结CD.若AB=7,AC=5,则△ACD的周长为( )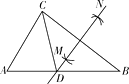
A.2 ![]()
B.12
C.17
D.19
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:已知:如图1,直线AB∥CD,现将直角三角板△PMN放入图中,其中∠MPN=90°,点P始终在直线MN右侧.PM交AB于点E,PN交CD于点F,试探究:∠PFD与∠AEM的数量关系.
(1)特例如图2,当点P在直线AB上(即点E与点P重合)时,直接写出∠PFD与∠AEM的数量关系,不必证明;
(2)类比探究:如图1,当点P在AB与CD之间时,猜想∠PFD与∠AEM的数量关系,并说明理由;
(3)拓展延伸:如图3,当点P在直线AB的上方时,PN交AB于点H,其他条件不变,猜想∠PFD与∠AEM的数量关系,并说明理由.
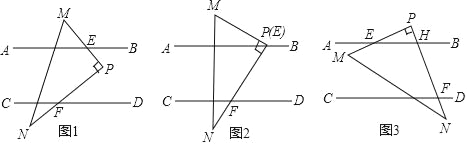
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某市市民晚饭后1小时内的生活方式,调查小组设计了“阅读”、“锻炼”、“看电视”和“其它”四个选项,用随机抽样的方法调查了该市部分市民,并根据调查结果绘制成如下统计图.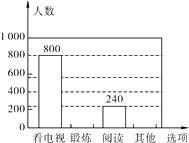
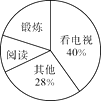
根据统计图所提供的信息,解答下列问题:
(1)本次共调查了名市民;
(2)补全条形统计图;
(3)该市共有480万市民,估计该市市民晚饭后1小时内锻炼的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.
甲公司方案:每月的养护费用y(元)与绿化面积x(平方米)是一次函数关系,如图所示.
乙公司方案:绿化面积不超过1000平方米时,每月收取费用5500元;绿化面积超过1000平方米时,每月在收取5500元的基础上,超过部分每平方米收取4元.

(1)求如图所示的y与x的函数解析式;(不要求写取值范围)
(2)如果某学校目前的绿化面积是1200平方米.试通过计算说明:选择哪家公司的服务,每月的绿化养护费用较少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com