
����Ŀ����ͼ������ABCD�У�AD��BC����BAD=90�㣬CE��AD�ڵ�E��AD=8cm��BC=4cm��AB=5cm���ӳ�ʼʱ�̿�ʼ������P��Q �ֱ�ӵ�A��Bͬʱ�������˶��ٶȾ�Ϊ1cm/s������P��A��B����C����E�ķ����˶�������Eֹͣ������Q��B����C����E����D�ķ����˶�������Dֹͣ�����˶�ʱ��Ϊxs����PAQ�����Ϊycm2 �� ������涨���߶������Ϊ0�������Σ�
����������⣺
��1����x=2sʱ��y=cm2����x= ![]() sʱ��y=cm2 ��
sʱ��y=cm2 ��
��2����5��x��14 ʱ����y��x֮��ĺ�����ϵʽ��
��3��������P���߶�BC���˶�ʱ����� ![]() S����ABCDʱx��ֵ��
S����ABCDʱx��ֵ��
��4��ֱ��д���������˶������У�ʹPQ���ı���ABCE�ĶԽ���ƽ�е�����x��ֵ��
���𰸡�
��1��2��9
��2��
�⣺��5��x��9ʱ����ͼ1��
y=S����ABCQ��S��ABP��S��PCQ= ![]() ��5+x��4����4
��5+x��4����4 ![]() ��5��x��5��
��5��x��5�� ![]() ��9��x����x��4��
��9��x����x��4��
y= ![]() x2��7x+
x2��7x+ ![]()
��9��x��13ʱ����ͼ2��
y= ![]() ��x��9+4����14��x��
��x��9+4����14��x��
y=�� ![]() x2+
x2+ ![]() x��35
x��35
��13��x��14ʱ����ͼ3��
y= ![]() ��8��14��x��
��8��14��x��
y=��4x+56��
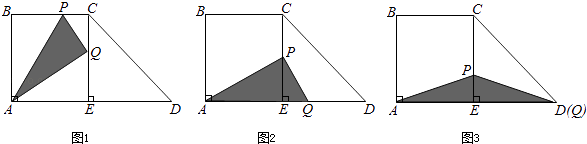
��3��
�⣺������P���߶�BC���˶�ʱ��
�� ![]() S����ABCD=
S����ABCD= ![]() ��
�� ![]() ��4+8����5=8
��4+8����5=8
��8= ![]() x2��7x+
x2��7x+ ![]() ����x2��14x+49=0����ã�x1=x2=7
����x2��14x+49=0����ã�x1=x2=7
�൱x=7ʱ�� ![]() S����ABCD
S����ABCD
��4��
�⣺���˶�ʱ��Ϊx�룬
��PQ��ACʱ��BP=5��x��BQ=x��
��ʱ��BPQ�ס�BAC��
�� ![]() =
= ![]() ����
���� ![]() =
= ![]() ��
��
���x= ![]() ��
��
��PQ��BEʱ��PC=9��x��QC=x��4��
��ʱ��PCQ�ס�BCE��
�� ![]() =
= ![]() ����
���� ![]() =
= ![]() ��
��
���x= ![]() ��
��
��PQ��BEʱ��EP=14��x��EQ=x��9��
��ʱ��PEQ�ס�BAE��
�� ![]() =
= ![]() ����
���� ![]() =
= ![]() ��
��
���x= ![]() ��
��
��������x��ֵΪ��x= ![]() ��
�� ![]() ��
�� ![]() ��
��
���������⣺��1����x=2sʱ��AP=2��BQ=2��
��y= ![]() =2
=2
��x= ![]() sʱ��AP=4.5��Q����EC��
sʱ��AP=4.5��Q����EC��
��y= ![]() =9
=9
���Դ��ǣ�2��9
�����㾫����������Ҫ���������������ε�Ӧ�õ����֪ʶ�㣬��Ҫ���ղ�ߣ��������ܵ��ﶥ��������ĸ߶ȣ�ͨ���á���ͬһʱ�������Ӱ���ɱ�������ԭ���������ࣺ�������ܵ��������ľ�����������������������������ȷ�����⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������Ĵ���װ�г���ɫ���������ͬ��n��С��������5�����Ӵ����������һ��������ɫ�����Ϊһ���������飬֮������Żش��У����Ⱥ��ټ�������һ�����������ü����ģ������������������������������б���
����������� | 100 | 1000 | 5000 | 10000 | 50000 | 100000 |
����������� | 46 | 487 | 2506 | 5008 | 24996 | 50007 |
�����б������Թ��Ƴ�n��ֵ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC����E��F�ֱ��DZ�AB��AC���е㣬��D�ڱ�BC�ϣ���DE=DF��AD=2��BC=6�����ı���AEDF���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB�ǡ�O��ֱ������C��D�ڡ�O�ϣ���E�ڡ�O�⣬��EAC=��B��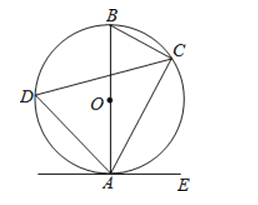
��1����֤��ֱ��AE�ǡ�O������
��2������D=60�㣬AB=6ʱ�����ӻ�![]() �ij�����������У�
�ij������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������ز���÷�����ļ��ڣ�ijˮ�������̵�������δ������г���������÷40�䣬��֪��һ�����ν����۷ֱ�Ϊÿ��50Ԫ��40Ԫ���ҵڶ��αȵ�һ�ζึ��700Ԫ��
��1�����һ�����ι�����÷�������ֱ�Ϊa�䡢b�䣬��a��b��ֵ��
��2�����̵����40����÷�Ȱ�ÿ��60Ԫ������x�䣬����İ�ÿ��35Ԫȫ�����꣮
�����̵�������ȫ����÷��������y��Ԫ����x���䣩֮��ĺ�����ϵʽ��
�ڵ�x��ֵ����Ϊ����ʱ���̵�Ų��������
��ע����������ۣ�����=���������멁�����ܳɱ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̽�������⣺
��֪��b����С������������a��b���㣨c��5��2+|a+b|��0����ش����⣺
��1����ֱ��д��a��b��c��ֵ��a���� ����b���� ����c���� ����
��2��������a��b��c����������Ӧ�ĵ�ֱ�ΪA��B��C����A��B��Cͬʱ��ʼ���������˶�������A��ÿ��1����λ���ȵ��ٶ������˶���ͬʱ����B�͵�C�ֱ���ÿ��1����λ���Ⱥ�3����λ���ȵ��ٶ������˶�������t���ӹ�������B���C֮��ľ����ʾΪBC����A���B֮��ľ����ʾΪAB����A���C֮��ľ����ʾΪAC��
��t���ӹ���AC�ij���Ϊ�� ������t�Ĺ�ϵʽ��ʾ����
�����ʣ�BC��AB��ֵ�Ƿ�����ʱ��t�ı仯���ı䣿���仯����˵�����ɣ������䣬������ֵ��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AB=AD=6��AB��BC��AD��CD����BAD=60�㣬��M��N�ֱ���AB��AD���ϣ���AM��MB=AN��ND=1��2���� cos��MCN= �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����9��9�������������У���ABC���������ڸ���ϣ�ÿ��С�����εı߳�Ϊ1��
��1�������ʵ���ƽ��ֱ������ϵ������A������Ϊ��1��1������C������Ϊ��4��2��������ƽ��ֱ������ϵ��д����B�����ꣻ
��2��ֱ��l������A����y��ƽ�У�д����B��C����ֱ��l�ԳƵ�B1��C1�����ꣻ
��3��ֱ��д��BC��һ��P��a��b������ֱ��l�ԳƵ�P1�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��CΪ�߶�AB��һ�㣬��DΪBC���е㣬��AB��18cm��AC��4CD��
��1��ͼ�й����� �����߶Σ�
��2����AC�ij���
��3������E��ֱ��AB�ϣ���EA��2cm����BE�ij���
![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com