
����Ŀ��̽�������⣺
��֪��b����С������������a��b���㣨c��5��2+|a+b|��0����ش����⣺
��1����ֱ��д��a��b��c��ֵ��a���� ����b���� ����c���� ����
��2��������a��b��c����������Ӧ�ĵ�ֱ�ΪA��B��C����A��B��Cͬʱ��ʼ���������˶�������A��ÿ��1����λ���ȵ��ٶ������˶���ͬʱ����B�͵�C�ֱ���ÿ��1����λ���Ⱥ�3����λ���ȵ��ٶ������˶�������t���ӹ�������B���C֮��ľ����ʾΪBC����A���B֮��ľ����ʾΪAB����A���C֮��ľ����ʾΪAC��
��t���ӹ���AC�ij���Ϊ�� ������t�Ĺ�ϵʽ��ʾ����
�����ʣ�BC��AB��ֵ�Ƿ�����ʱ��t�ı仯���ı䣿���仯����˵�����ɣ������䣬������ֵ��
![]()
���𰸡�(1)a=��1��b=1��c=5��(2)��6+4t����BC��AB��ֵ�Dz�����ʱ��t�ı仯���ı䣬��ֵΪ2��
��������
��1������bΪ��С�����������b��ֵ�����ɷǸ����ĺ͵����ʽ������̾Ϳ������a��b��ֵ��
��2�����ȷֱ��ʾ��t���ӹ���A��C��λ�ã���������������֮��ľ��빫ʽ�Ϳ���������ۣ�
���ȸ�������������֮��ľ��빫ʽ�ֱ��ʾ��BC��AB�Ϳ��Եó�BC-AB��ֵ�������
(1)��b��������������
��b=1��
�ߣ�c��5��2+|a+b|=0��
��![]()
��![]()
�ʴ�Ϊ��a=��1��b=1��c=5��
(2)�������⣬��
t��������A���ʾ����Ϊ����1��t��C���ʾ����Ϊ��5+3t��
��AC=5+3t������1��t��=6+4t��
�ʴ�Ϊ��6+4t��
�������⣬��
BC=4+2t��AB=2+2t��
��BC��AB=4+2t����2+2t��=2��
��BC��AB��ֵ�Dz�����ʱ��t�ı仯���ı䣬��ֵΪ2��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A����4��![]() ����B����1��2����һ�κ���y1=ax+b�뷴��������y2=
����B����1��2����һ�κ���y1=ax+b�뷴��������y2=![]() ͼ����������㣬AC��x���ڵ�C��BD��y���ڵ�D��
ͼ����������㣬AC��x���ڵ�C��BD��y���ڵ�D��
��1������ͼ��ֱ�ӻش��ڵڶ������ڣ���xȡ��ֵʱ��y1��y2��0��
��2����һ�κ�������ʽ��m��ֵ��
��3��P���߶�AB��һ�㣬����PC��PD������PCA�͡�PDB�����ȣ����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ACB=90�㣬�ֱ��Ե�A��BΪԲ�ģ�����ͬ�ij�������![]() AB��Ϊ�뾶�����������ཻ�ڵ�M��N����ֱ��MN��AB�ڵ�D����BC�ڵ�E������CD�����н��۴�����ǣ�������
AB��Ϊ�뾶�����������ཻ�ڵ�M��N����ֱ��MN��AB�ڵ�D����BC�ڵ�E������CD�����н��۴�����ǣ�������
A.AD=BD
B.BD=CD
C.��A=��BED
D.��ECD=��EDC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǰ�ԲO��ֱ����C��AB�ӳ����ϵ�һ�㣬CD���ԲO�����ڵ�D������AD��BD��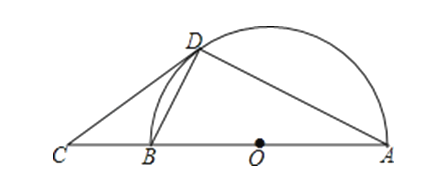
��1����֤����BAD=��BDC��
��2������BDC=28�㣬BD=2�����O�İ뾶������ȷ��0.01��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AD��BC����BAD=90�㣬CE��AD�ڵ�E��AD=8cm��BC=4cm��AB=5cm���ӳ�ʼʱ�̿�ʼ������P��Q �ֱ�ӵ�A��Bͬʱ�������˶��ٶȾ�Ϊ1cm/s������P��A��B����C����E�ķ����˶�������Eֹͣ������Q��B����C����E����D�ķ����˶�������Dֹͣ�����˶�ʱ��Ϊxs����PAQ�����Ϊycm2 �� ������涨���߶������Ϊ0�������Σ�
����������⣺
��1����x=2sʱ��y=cm2����x= ![]() sʱ��y=cm2 ��
sʱ��y=cm2 ��
��2����5��x��14 ʱ����y��x֮��ĺ�����ϵʽ��
��3��������P���߶�BC���˶�ʱ����� ![]() S����ABCDʱx��ֵ��
S����ABCDʱx��ֵ��
��4��ֱ��д���������˶������У�ʹPQ���ı���ABCE�ĶԽ���ƽ�е�����x��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ABC=90�㣬AB=BC=![]() ������ABC�Ƶ�C��ʱ����ת60�㣬�õ���MNC������BM����BM�ij��� .
������ABC�Ƶ�C��ʱ����ת60�㣬�õ���MNC������BM����BM�ij��� .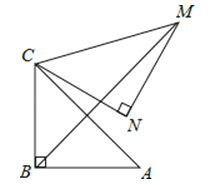
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��������������1������1�������n��������Щ�����ɫ�����������
��1����n=1ʱ���Ӵ����������1���������������������Ŀ������Ƿ���ͬ�����ڴ����Ӧλ�����ͬ������ͬ������
��2���Ӵ����������һ����¼����ɫ��Ȼ��Żأ������ظ���ʵ�飬�������������Ƶ���ȶ���0.25����n��ֵ��
��3����һ��������Ϸ�У����п��ܳ��ֵĽ�����£�
������״ͼ���ֵĽ��������������������ɫ��ͬ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ⲻ��ʽ�� ![]() ����������գ���ɱ���Ľ��
����������գ���ɱ���Ľ��
���ⲻ��ʽ�٣�����
���ⲻ��ʽ�ڣ�����
���Ѳ���ʽ�ٺ͢ڵĽ��������ϱ�ʾ������
������ԭ����ʽ��Ľ⼯Ϊ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
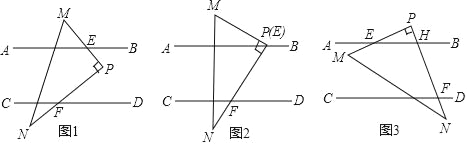
����Ŀ�������龳����֪����ͼ1��ֱ��AB��CD���ֽ�ֱ�����ǰ��PMN����ͼ�У����С�MPN=90������Pʼ����ֱ��MN�Ҳ࣮PM��AB�ڵ�E��PN��CD�ڵ�F����̽������PFD���AEM��������ϵ��
��1��������ͼ2������P��ֱ��AB�ϣ�����E���P�غϣ�ʱ��ֱ��д����PFD���AEM��������ϵ������֤����
��2�����̽������ͼ1������P��AB��CD֮��ʱ�������PFD���AEM��������ϵ����˵�����ɣ�
��3����չ���죺��ͼ3������P��ֱ��AB���Ϸ�ʱ��PN��AB�ڵ�H�������������䣬�����PFD���AEM��������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com