
【题目】如图①,在锐角△ABC中,D,E分别为AB,BC中点,F为AC上一点,且∠AFE=∠A,DM∥EF交AC于点M.
(1)求证:DM=DA;
(2)点G在BE上,且∠BDG=∠C,如图②,求证:△DEG∽△ECF;
(3)在图②中,取CE上一点H,使∠CFH=∠B,若BG=1,求EH的长.
【答案】
(1)
证明:如图1所示,
∵DM∥EF,
∴∠AMD=∠AFE,
∵∠AFE=∠A,
∴∠AMD=∠A,
∴DM=DA;
(2)
证明:如图2所示,
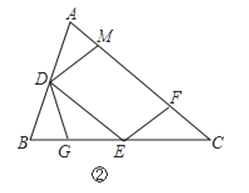
∵D、E分别是AB、BC的中点,
∴DE∥AC,
∴∠BDE=∠A,∠DEG=∠C,
∵∠AFE=∠A,
∴∠BDE=∠AFE,
∴∠BDG+∠GDE=∠C+∠FEC,
∵∠BDG=∠C,
∴∠DGE=∠FEC,
∴△DEG∽△ECF;
(3)
解:如图3所示,
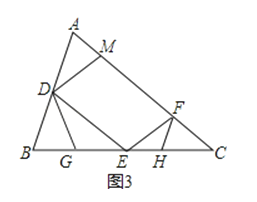
∵∠BDG=∠C=∠DEB,∠B=∠B,
∴△BDG∽△BED,
∴![]() ,
,
∴BD2=BGBE,
∵∠AFE=∠A,∠CFH=∠B,
∴∠C=180°﹣∠A﹣∠B=180°﹣∠AFE﹣∠CFH=EFH,
又∵∠FEH=∠CEF,
∴△EFH∽△ECF,
∴![]() ,
,
∴EF2=EHEC,
∵DE∥AC,DM∥EF,
∴四边形DEFM是平行四边形,
∴EF=DM=DA=BD,
∴BGBE=EHEC,
∵BE=EC,
∴EH=BG=1.
【解析】(1)证明∠A=∠DMA,用等角对等边即可证明结论;
(2)由D、E分别是AB、BC的中点,可知DE∥AC,于是∠BDE=∠A,∠DEG=∠C,又∠A=∠AFE,∠AFE=∠C+∠FEC,根据等式性质得∠FEC=∠GDE,根据有两对对应角相等的两三角形相似可证;
(3)通过证明△BDG∽△BED和△EFH∽△ECF,可得BGBE=EHEC,又BE=EC,所以EH=BG=1.
此题考查了相似三角形的判定与性质.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点E,F分别是边AB,AC的中点,点D在边BC上.若DE=DF,AD=2,BC=6,求四边形AEDF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若AM:MB=AN:ND=1:2.则 cos∠MCN= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在9×9的正方形网格中,△ABC三个顶点在格点上,每个小正方形的边长为1.
(1)建立适当的平面直角坐标系后,若点A的坐标为(1,1),点C的坐标为(4,2),画出平面直角坐标系并写出点B的坐标;
(2)直线l经过点A且与y轴平行,写出点B、C关于直线l对称点B1、C1的坐标;
(3)直接写出BC上一点P(a,b)关于直线l对称点P1的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次初中生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下的统计图①和图②,请根据相关信息,解答下列问题: 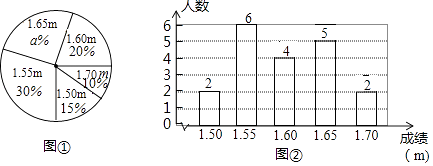
(1)①中a的值为;
(2)统计的这组初赛成绩数据的平均数、众数和中位数(结果保留小数点后两位);
(3)据这组初赛成绩,由高到低确定7人进入复赛,请直接写出初赛成绩为1.60m的运动员能否进入复赛.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2﹣4x与x轴交于O,A两点,P为抛物线上一点,过点P的直线y=x+m与对称轴交于点Q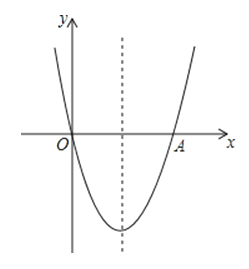
(1)这条抛物线的对称轴是 ,直线PQ与x轴所夹锐角的度数是 .
(2)若两个三角形面积满足S△POQ=![]() S△PAQ , 求m的值
S△PAQ , 求m的值
(3)当点P在x轴下方的抛物线上时,过点C(2,2)的直线AC与直线PQ交于点D,求:①PD+DQ的最大值;②PDDQ的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,东营市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如图两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题: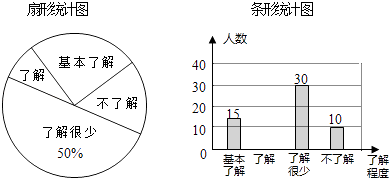
(1)接受问卷调查的学生共有 人,扇形统计图中“基本了解”部分所对应扇形的圆心角为 ;
(2)请补全条形统计图;
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数;
(4)若从对校园安全知识达到了“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AB上一点,点D为BC的中点,且AB=18cm,AC=4CD.
(1)图中共有 条线段;
(2)求AC的长;
(3)若点E在直线AB上,且EA=2cm,求BE的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的边AB是⊙O的直径,点C在⊙O上,已知AC=6cm,BC=8cm,点P、Q分别在边AB、BC上,且点P不与点A、B重合,BQ=kAP(k>0),联接PC、PQ. 
(1)求⊙O的半径长;
(2)当k=2时,设AP=x,△CPQ的面积为y,求y关于x的函数关系式,并写出定义域;
(3)如果△CPQ与△ABC相似,且∠ACB=∠CPQ,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com