
如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是 的中点,则下列结论不成立的是( )
的中点,则下列结论不成立的是( )

A.OC∥AE B.EC=BC C.∠DAE=∠ABE D.AC⊥OE
D
【解析】由C为弧EB的中点,利用垂径定理的逆定理得出OC垂直于BE,由AB为圆的直径,利用直径所对的圆周角为直角得到AE垂直于BE,即可确定出OC与AE平行,选项A正确;
由C为弧BE中点,即弧BC=弧CE,利用等弧对等弦,得到BC=EC,选项B正确;
由AD为圆的切线,得到AD垂直于OA,进而确定出一对角互余,再由直角三角形ABE中两锐角互余,利用同角的余角相等得到∠DAE=∠ABE,选项C正确;
AC不一定垂直于OE,选项D错误.
【解析】
A、∵点C是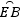 的中点,∴OC⊥BE,∵AB为圆O的直径,∴AE⊥BE,∴OC∥AE,本选项正确;
的中点,∴OC⊥BE,∵AB为圆O的直径,∴AE⊥BE,∴OC∥AE,本选项正确;
B、∵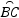 =
=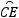 ,∴BC=CE,本选项正确;
,∴BC=CE,本选项正确;
C、∵AD为圆O的切线,∴AD⊥OA,∴∠DAE+∠EAB=90°,∵∠EBA+∠EAB=90°,∴∠DAE=∠EBA,本选项正确;
D、AC不一定垂直于OE,本选项错误.
故选D.


科目:初中数学 来源:2014中考名师推荐数学立体图形(解析版) 题型:填空题
如图,圆柱形容器中,高为1.2m,底面周长为1m,在容器内壁离容器底部0.3m的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为 m(容器厚度忽略不计).

查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学数形结合思想(解析版) 题型:选择题
数形结合是数学中常用的思想方法,试运用这一思想方法确定函数y=x2+1与y=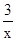 的交点的横坐标x0的取值范围是( )
的交点的横坐标x0的取值范围是( )
A.0<x0<1
B.1<x0<2
C.2<x0<3
D.﹣1<x0<0
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学圆(解析版) 题型:解答题
如图,在平面直角坐标系中,O为坐标原点,点A、B的坐标分别为(8,0)、(0,6).动点Q从点O、动点P从点A同时出发,分别沿着OA方向、AB方向均以1个单位长度/秒的速度匀速运动,运动时间为t(秒)(0<t≤5).以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连接CD、QC.
(1)求当t为何值时,点Q与点D重合?
(2)设△QCD的面积为S,试求S与t之间的函数关系式,并求S的最大值;
(3)若⊙P与线段QC只有一个交点,请直接写出t的取值范围.

查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学圆(解析版) 题型:填空题
如图,AB是⊙O的直径,弦BC=4cm,F是弦BC的中点,∠ABC=60°.若动点E以1cm/s的速度从A点出发在AB上沿着A→B→A运动,设运动时间为t(s)(0≤t<16),连接EF,当△BEF是直角三角形时,t(s)的值为 .(填出一个正确的即可)

查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学圆(解析版) 题型:选择题
如图,AB为⊙O的直径,C为⊙O外一点,过点C作⊙O切线,切点为B,连结AC交⊙O于D,∠C=38°.点E在AB右侧的半圆上运动(不与A、B重合),则∠AED的大小是( )

A.19°
B.38°
C.52°
D.76°
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学图形的折叠(解析版) 题型:填空题
如图,在△ABC中,AB=AC,BC=8,tanC=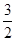 ,如果将△ABC沿直线l翻折后,点B落在边AC的中点处,直线l与边BC交于点D,那么BD的长为 .
,如果将△ABC沿直线l翻折后,点B落在边AC的中点处,直线l与边BC交于点D,那么BD的长为 .
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学分式方程(解析版) 题型:解答题
佳佳果品店在批发市场购买某种水果销售,第一次用1200元购进若干千克,并以每千克8元出售,很快售完.由于水果畅销,第二次购买时,每千克的进价比第一次提高了10%,用1452元所购买的数量比第一次多20千克,以每千克9元售出100千克后,因出现高温天气,水果不易保鲜,为减少损失,便降价50%售完剩余的水果.
(1)求第一次水果的进价是每千克多少元?
(2)该果品店在这两次销售中,总体上是盈利还是亏损?盈利或亏损了多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com