
【题目】如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F,且BF=BC.⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD,FH. 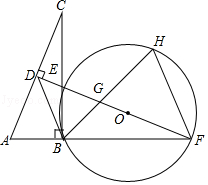
(1)求证:△ABC≌△EBF;
(2)试判断BD与⊙O的位置关系,并说明理由;
(3)若AB=1,求HGHB的值.
【答案】
(1)证明:∵DF⊥AC,△ABC为Rt△,
∴∠CDE=∠EBF=90°
∵∠CED=∠FEB,
∴∠DCE=∠EFB,
在△ABC和△EBF中,
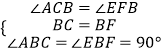 ,
,
∴△ABC≌△EBF,(ASA)
(2)解:结论:BD与⊙O相切.
理由:连接OB,
∵DF是AB的中垂线,∠ABC=90°,
∴DB=DC=DA,
∴∠DBC=∠C.
由(1)∠DCB=∠EFB,而∠EFB=∠OBF,
∴∠DBC=∠OBF,
∴∠DBO=∠DBC+∠EBO=∠OBF+∠EBO=90°,
∴DB⊥OB,
∴BD与⊙O相切
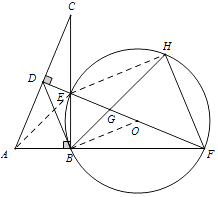
(3)解:连接EH,
∵BH是∠EBF的平分线,
∴∠EBH=∠HBF=45°.∠HFE=∠HBE=45°.
又∠GHF=∠FHB,
∴△GHF∽△FHB,
∴ ![]() =
= ![]() ,
,
∴HGHB=HF2,
∵⊙O是Rt△BEF的内接圆,
∴EF为⊙O的直径,
∴∠EHF=90°,
又∠HFE=45°,
∴EH=HF,
∴EF2=EH2+HF2=2HF2,
在Rt△ABC中,AB=1,tan∠C= ![]() ,
,
∴BC=2,AC= ![]() ,
,
由(1)知△ABC≌△EBF,
∴EF=AC= ![]() ,
,
∴2HF2=EF2=5,
∴HF2= ![]() ,
,
故HGHB=HF2= ![]()

【解析】(1)根据ASA或AAS即可证明;(2)结论:BD与⊙O相切. 连接OB,只要证明OB⊥BD即可;(3)连接EH,首先证明△GHF∽△FHB,可得 ![]() =
= ![]() ,即HGHB=HF2 , 想办法求出HF2即可解决问题.
,即HGHB=HF2 , 想办法求出HF2即可解决问题.


 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:
【题目】几何计算:
(1)如图:已知AB=9cm,BD=3cm,C为AB的中点,求线段DC的长.
![]()
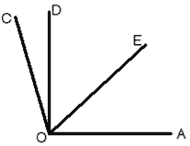
(2)如图,OE为∠AOD的平分线,∠COD=![]() ∠EOC,∠COD=15°,求:
∠EOC,∠COD=15°,求:
①∠EOC的大小;
②∠AOD的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算.
(1)( x-y)7÷(y-x)2÷( x-y)3;
(2) ![]() +
+![]() +
+![]() ;
;
(3)( -2)0- ![]() +
+![]() +
+![]() ·
·![]() ;
;
(4) a4m+1÷(-a) 2m+1 (m为正整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一堆有红、白两种颜色的球若干个,已知白球的个数比红球少,但白球的2倍比红球多.若把每一个白球都记作“2”,每一个红球都记作“3”,则总数为“60”,那么这两种球各有多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】1或5 △ABC中,AB=AC=12厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v的值为

A. 2 B. 3 C. 2或3 D. 1或5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,AC=BC=2,正方形CDEF的顶点D、F分别在AC、BC边上,设CD的长度为x,△ABC与正方形CDEF重叠部分的面积为y,则下列图象中能表示y与x之间的函数关系的是( )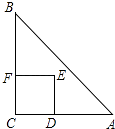
A.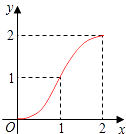
B.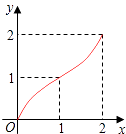
C.
D.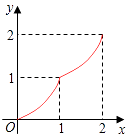
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上点A表示的数为﹣2,点B表示的数为8,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒(t>0).
(1)填空:
①A、B两点间的距离AB= ,线段AB的中点表示的数为 ;
②用含t的代数式表示:t秒后,点P表示的数为 ;点Q表示的数为 .
(2)求当t为何值时,PQ=![]() AB;
AB;
(3)当点P运动到点B的右侧时,PA的中点为M,N为PB的三等分点且靠近于P点,求PM﹣![]() BN的值.
BN的值.
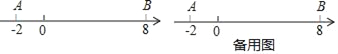
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF= ![]() ∠CAB.
∠CAB. 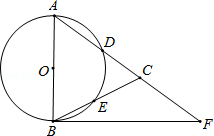
(1)求证:直线BF是⊙O的切线;
(2)若AB=5,sin∠CBF= ![]() ,求BC和BF的长.
,求BC和BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点A(0,6)的直线AB与直线OC相交于点C(2,4)动点P沿路线O→C→B运动.(1)求直线AB的解析式;(2)当△OPB的面积是△OBC的面积的![]() 时,求出这时点P的坐标;(3)是否存在点P,使△OBP是直角三角形?若存在,直接写出点P的坐标,若不存在,请说明理由.
时,求出这时点P的坐标;(3)是否存在点P,使△OBP是直角三角形?若存在,直接写出点P的坐标,若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com