
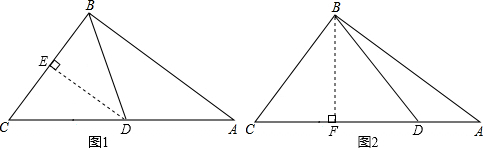
 ��ͼ����Rt��ABC�У���ABC=90�㣬AB=8��BC=6����DΪAC���ϵĶ��㣬��D�ӵ�C�������ر�CA���A�˶������˶�����Aʱֹͣ�������D�˶���ʱ��Ϊt�룮��D�˶����ٶ�Ϊÿ��1����λ���ȣ�
��ͼ����Rt��ABC�У���ABC=90�㣬AB=8��BC=6����DΪAC���ϵĶ��㣬��D�ӵ�C�������ر�CA���A�˶������˶�����Aʱֹͣ�������D�˶���ʱ��Ϊt�룮��D�˶����ٶ�Ϊÿ��1����λ���ȣ����� ��1������CD=�ٶȡ�ʱ����ʽ���㼴�ɵý⣬���ù��ɶ�����ʽ���AC���ٸ���AD=AC-CD�������ݽ��м��㼴�ɵý⣻
��2���֢١�CDB=90��ʱ�����á�ABC�������ʽ���㼴�����BD��Ȼ�����ù��ɶ�����ʽ���õ�CD���ٸ���ʱ��=·�̡��ٶȼ��㣻�ڡ�CBD=90��ʱ����D�͵�A�غϣ�Ȼ�����ʱ��=·�̡��ٶȼ��㼴�ɵý⣻
��3���֢�CD=BCʱ��CD=6����BD=BCʱ������B��BF��AC��F�����ݵ������������ߺ�һ�����ʿɵ�CD=2CF�����ɣ�2���Ľ��۽��
���  �⣺��1��t=2ʱ��CD=2��1=2��
�⣺��1��t=2ʱ��CD=2��1=2��
�ߡ�ABC=90�㣬AB=8��BC=6��
��AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{8}^{2}+{6}^{2}}$=10��
AD=AC-CD=10-2=8��
�ʴ��ǣ�2��8��
��2���١�CDB=90��ʱ��S��ABC=$\frac{1}{2}$AC•BD=$\frac{1}{2}$AB•BC��
��$\frac{1}{2}$��10•BD=$\frac{1}{2}$��8��6��
���BD=4.8��
��CD=$\sqrt{B{C}^{2}-B{D}^{2}}$=$\sqrt{{6}^{2}-4��{8}^{2}}$=3.6��
t=3.6��1=3.6�룻
�ڡ�CBD=90��ʱ����D�͵�A�غϣ�
t=10��1=10�룬
����������t=3.6��10�룻
�ʴ�Ϊ����1��2��8����2��3.6��10�룻
��3����CD=BCʱ��CD=6��t=6��1=6��
��BD=BCʱ����ͼ2������B��BF��AC��F��
��CF=3.6��
CD=2CF=3.6��2=7.2��
��t=7.2��1=7.2��
����������t=6���7.2��ʱ����CBD����BD��CDΪ�ĵ��������Σ�
���� ���⿼���˹��ɶ��������������ε��ж������ʣ������ε��������2����3���ѵ�����Ҫ��������ۣ�����ͼ�θ�����ֱ�ۣ�


 ������ʱͬ����ϰ��ϵ�д�
������ʱͬ����ϰ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
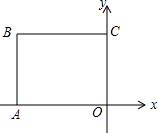 ��ͼ��OΪ����ԭ�㣬����OABC�У�A��-8��0����C��0��6����������OABC�Ƶ�O��ת60�㣬�õ�����OA��B��C�䣬��ʱֱ��OA����ֱ��BC�ཻ��P�����P������Ϊ��-2$\sqrt{3}$��6����2$\sqrt{3}$��6����
��ͼ��OΪ����ԭ�㣬����OABC�У�A��-8��0����C��0��6����������OABC�Ƶ�O��ת60�㣬�õ�����OA��B��C�䣬��ʱֱ��OA����ֱ��BC�ཻ��P�����P������Ϊ��-2$\sqrt{3}$��6����2$\sqrt{3}$��6�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
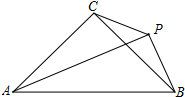 ��ͼ����ABCΪ����ֱ�������Σ�AC��BC��PA��PB������PC��
��ͼ����ABCΪ����ֱ�������Σ�AC��BC��PA��PB������PC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
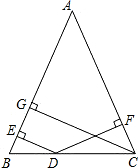 ��ͼ���ڡ�ABC�У�AB=AC��D��BC������һ�㣬��D�ֱ���AB��AC�����ߣ�����ֱ�ΪE��F��CG��AB���ϵĸߣ�
��ͼ���ڡ�ABC�У�AB=AC��D��BC������һ�㣬��D�ֱ���AB��AC�����ߣ�����ֱ�ΪE��F��CG��AB���ϵĸߣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2�� | B�� | 3�� | C�� | 4�� | D�� | 5�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com