
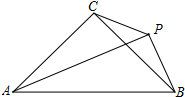
 如图,△ABC为等腰直角三角形,AC⊥BC,PA⊥PB,连接PC.
如图,△ABC为等腰直角三角形,AC⊥BC,PA⊥PB,连接PC.分析 (1)在RT△ABC中,利用勾股定理即可解决.
(2)如图1中,作CE⊥CP交AP于E,利用四点共圆得∠CPA=∠CBA=45°,由△ACE≌△BCP得AE=PB,由此即可解决.
(3)如图3,延长BP、AC交于E,作FM⊥AB,PN⊥BC垂足分别为M、N,由PN∥AC得$\frac{PF}{AF}=\frac{PN}{AC}$设FC=FM=BM=a,则FB=$\sqrt{2}$a,AC=BC=($\sqrt{2}$+1)a,求出PN即可解决问题.
解答 (1)解:设CB=AC=a,在RT△ACB中,∵∠ACB=90°,AB=2,
∴a2+a2=22,
∴a2=2,
∵a>0,
∴a=$\sqrt{2}$.
∴AC=$\sqrt{2}$.
(2)证明:如图1中,作CE⊥CP交AP于E,
∵∠ACB=∠APB=90°,
∴A、B、P、C四点共圆,
∴∠CPA=∠CBA=45°,
∵∠ACB=∠ECP=90°,
∴∠ACE=∠BCP,∠CEP=∠CPE=45°,
∴∠AEC=∠CPB=135°,
在△ACE和△BCP中,
$\left\{\begin{array}{l}{∠ACE=∠BCP}\\{∠AEC=∠CPB}\\{AC=BC}\end{array}\right.$,
∴△ACE≌△BCP,
∴AE=PB,
∴PA-PB=PA-AE=PE=$\sqrt{2}$PC.
(3)解:如图3,延长BP、AC交于E,作FM⊥AB,PN⊥BC垂足分别为M、N.
∵CA=CB,∠ACB=∠FMB=90°,
∴∠ABC=∠MFB=45°,
∴MF=MB,
∵AF平分∠CAB,
∴FC=FM=BM,设FC=FM=BM=a,则FB=$\sqrt{2}$a,AC=BC=($\sqrt{2}$+1)a,
在△ACF和△BCE中,
$\left\{\begin{array}{l}{∠ACF=∠BCE}\\{AC=BC}\\{∠CAF=∠CBE}\end{array}\right.$,
∴△ACF≌△BCE,
∴CF=CE=a,
在△APE和△APB中,
$\left\{\begin{array}{l}{∠PAE=∠PAB}\\{AP=AP}\\{∠APE=∠APB}\end{array}\right.$,
∴△APE≌△APB,
∴PE=PB,
∵∠PNB=∠ECB=90°,
∴PN∥AE,∵PB=PE,
∴NC=NB,
∴PN=$\frac{1}{2}EC$=$\frac{1}{2}$a.
∵PN∥AC,
∴$\frac{PF}{AF}=\frac{PN}{AC}$=$\frac{\frac{1}{2}a}{(\sqrt{2}+1)a}$=$\frac{\sqrt{2}-1}{2}$.
点评 本题考查全等三角形的判定和性质、等腰直角三角形的性质、角平分线的性质、四点共圆等知识,解题的关键是利用四点共圆发现∠CPA=45°,学会常用的添加辅助线的方法,属于中考常考题型.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,点D为AC边上的动点,点D从点C出发,沿边CA向点A运动,当运动到点A时停止,若设点D运动的时间为t秒.点D运动的速度为每秒1个单位长度.
如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,点D为AC边上的动点,点D从点C出发,沿边CA向点A运动,当运动到点A时停止,若设点D运动的时间为t秒.点D运动的速度为每秒1个单位长度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com