【题目】如图，小华剪了两条宽均为
的纸条，交叉叠放在一起，且它们的交角为
，则它们重叠部分的面积为（ ）
A. 
B. 
C. 
D. 
【答案】D
【解析】
过A作AE⊥BC于E，AF⊥CD于F，则AE=AF=
，∠AEB=∠AFD=90°，求出四边形ABCD是平行四边形，证出△AEB≌△AFD，推出AB=AD，求出四边形ABCD是菱形，根据菱形的性质得出AB=BC，解直角三角形求出AB，根据菱形的面积公式求出即可．
过A作AE⊥BC于E，AF⊥CD于F，则AE=AF=，∠AEB=∠AFD=90°．
∵AD∥BC，AB∥CD，∴四边形ABCD是平行四边形，∴∠ABE=∠ADF=60°．
在△AEB和△AFD中，∵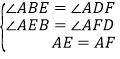
，∴△AEB≌△AFD，∴AB=AD，∴四边形ABCD是菱形，∴AB=BC．
在Rt△AEB中，∠AEB=90°，AE=，∠ABE=60°，∴BE=
=1，AB=
=2，∴BC=AB=2，∴重叠部分的面积是BC×AE=2．
故选D．
提分百分百检测卷系列答案科目：初中数学 来源： 题型：
【题目】如图，已知顶点为（－3，－6）的抛物线
经过点（－1，－4），下列结论：①b2＞4ac；②ax2+bx+c≥－6；③若点（－2，m），（－5，n）在抛物线上，则m＞n；④关于x的一元二次方程
的两根为﹣5和﹣1，其中正确的有（ ）
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点F、B、E、C在同一直线上，并且BF=CE，∠ABC=∠DEF．能否由上面的已知条件证明△ABC≌△DEF？如果能，请给出证明；如果不能，请从下列三个条件中选择一个合适的条件，添加到已知条件中，使△ABC≌△DEF，并给出证明．
提供的三个条件是：①AB=DE；②AC=DF；③AC∥DF．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，有一枚质地均匀的正十二面体形状的骰子，其中
个面标有“
”，个面标有“”，
个面标有“”，
个面标有“”，
个面标有“”，其余的面标有“
”，将这枚骰子掷出后：
①”
”朝上的概率是；②“”朝上的概率最大；③“”朝上的概率和“”朝上的概率一样大；
④“”朝上的概率是
．以上说法正确的有________．（填序号）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某村为增加蔬菜的种植面积，一年中修建了一些蔬菜大棚．平均修建每公顷大棚要用的支架、塑料膜等材料的费用为
元，此外还要购置喷灌设备，这项费用（元）与大棚面积（公顷）的平方成正比，比例系数为
．每公顷大棚的年平均经济收益为
元，这个村一年中由于修建蔬菜大棚而增加的收益（扣除修建费用后）为
元．
一年中这个村修建了多少公顷蔬菜大棚？
若要使收益达到最大，请问应修建多少公顷大棚？并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）如图1，点
是等腰三角形
的底边
上的一个动点，过点作的垂线，交直线
于点
，交
的延长线于点
，请观察
与
，它们有何数量关系？并证明你的猜想.
（2）如果点沿着底边所在的直线，按由
向
的方向运动到
的延长线上时，（1）中所得的结论还成立吗？请你在图2中完成图形，写出结论.并证明你的猜想.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】
年中秋节前夕，某代理商从厂家购进某品牌月饼的
、
两种礼盒，已知购进 种月饼
盒、 种月饼
盒共
元，购进
盒 种月饼比购进盒种多用
元．
(1)求、两种月饼礼盒的进价；
(2)若该代理商购进该品牌的这两种礼盒月饼资金不超过
元，购进盒数共
盒，且购进种礼盒的数量不超过种礼盒数量的
倍，共有几种进货方案？销售时，销售一盒种礼盒月饼可获利
元，销售一盒种礼盒月饼可获利
元，并全部售完，请直接写出获利最多的进货方案以及最大利润.
查看答案和解析>>
科目：初中数学 来源： 题型：
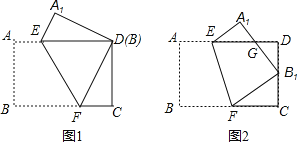
【题目】已知矩形纸片ABCD中，AB=2，BC=3.
操作：将矩形纸片沿EF折叠，使点B落在边CD上．
探究：⑴如图1，若点B与点D重合，你认为
和
全等吗？如果全等，请给出证明，如果不全等，请说明理由；
⑵如图2，若点B与CD的中点重合，请你判断
和
之间的关系，如果全等，只需写出结果，如果相似，请写出结果和相应的相似比；
⑶如图2，请你探索，当点B落在CD边上何处，即
的长度为多少时，
与
全等．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,在长方形ABCD中,AB=8, BC=4,将长方形的一角沿AC折叠,则重叠阴影部分△AFC的面积为( )
A. 14B. 12C.10D. 8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com